四角形ABCDにおいて、3辺の長さをそれぞれ AB = 5 , BC = 9 , CD = 3 、対角線 AC の長さを AC = 6 とする。このとき
cos ∠ABC = √ ア イ , sin ∠ABC = √ ウ √ エ オ
である。
ここで、四角形ABCDは台形であるとする。
次の カ には下の⓪~②から、 キ には③・④から当てはまるものを一つずつ選べ。
CD カ AB・sin∠ABC であるから キ である。
⓪ < ① = ② >
③ 辺ADと辺BCが平行 ④ 辺ABと辺CDが平行
したがって
BD = ク √ ケコ
である。
解答
アイウエオ
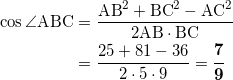
であり、
![]()
となる。
カキ
![]()
より、カには ⓪ が入る。
図形を考えて、④辺ABと辺CDが平行でなければならない。

コメント