 大学入試数学演習
大学入試数学演習 大学入試数学演習
 大学入試数学演習
大学入試数学演習  大学入試数学演習
大学入試数学演習 n回目に4色目が出る確率[2021 京都大・理]
 整数・証明・計算問題
整数・証明・計算問題 1000以下の素数は250個以下である[2021 一橋大]
 大学入試数学演習
大学入試数学演習 数列の和に関する性質[2006 東京大・理(後)]
 大学入試数学演習
大学入試数学演習 ユークリッドの互除法[2018 首都大学東京・理・数理科]
 大学入試数学演習
大学入試数学演習 対数螺旋の性質[2000 神戸大・理(後)]
 大学入試数学演習
大学入試数学演習 等確率でないサイコロ [1979 京都大・文理]
 大学入試数学演習
大学入試数学演習 2015Cmが偶数になる最小のm [2015 東京大・理]
 大学入試数学演習
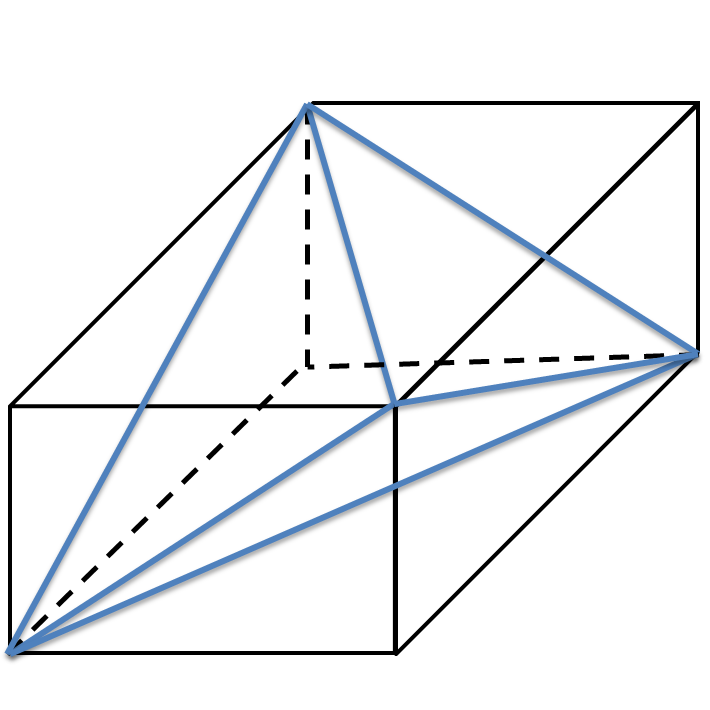
大学入試数学演習 等面四面体 [2014 早稲田大・教育]
 大学入試数学演習
大学入試数学演習