単調有界な数列の極限［2016 九州大・理（後）］

　正の実数 a , b に対して $A(a,b) = \dfrac{a+b}{2},G(a,b) = \sqrt{ab}$ とする。以下の問いに答えよ。
(1)　min ( a , b ) ≦ G ( a , b ) ≦ A ( a , b ) ≦ max ( a , b ) が成り立つことを示せ。
　ただし、 min ( a , b )は a , b のうちの最小の数を表し、 max ( a , b ) は a, b のうちの最大の数を表す（ a = b の場合は a , b のうちのどちらかの数を表すとする）。
(2)　a > b , a₀ = a , b₀ = b として、以下の数列を定義する。

$a_{n+1} = \frac{a_n + b_n}{2} , b_{n+1} = \sqrt{a_n b_n} , c_{n+1} = \frac{a_n - b_n}{2} , n = 0 ,1,2,\cdots$

このとき数列 { a_n } と数列 { b_n } は同じ極限値（αとする）に収束することを示せ。
(3)　a_n+2 を a_n と b_n を用いて表せ。ただし { a_n } と { b_n } は(2)で定義した数列とする。
(4)　c_n+2 と c_n+1 の間に以下の関係が成り立つことを示せ。ただし、 { c_n } とαはそれぞれ(2)で定義した数列と極限値とする。

$c_{n+2} < \left( \frac{1}{2\sqrt{\alpha}} c_{n+1} \right)^2$

［2016 九州大・理（後）］

イズミの解答への道

解答

(1)　a ≦ b としても一般性を失わない。

$\begin{align*} &\text{max} ( a , b ) - A ( a , b ) = b - \dfrac{a+b}{2} = \frac{b-a}{2} \geqq 0 \\ &A (a , b ) = G (a,b) = \frac{a+b}{2} - \sqrt{ab} = \frac{(\sqrt{a} - \sqrt{b})^2}{2} \geqq 0 \\ &G(a,b) - \text{min}(a,b) = \sqrt{ab} - a = \sqrt{a}(\sqrt{b} - \sqrt{a} ) \geqq 0 \end{align*}$

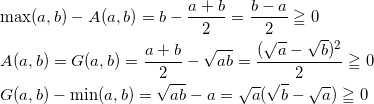
であるから、題意は示された。（なお、等号成立はすべての不等号について a = b のとき。）

(2)　まず、

(a) $b \leqq b_n < b_{n+1} < a_{n+1} < a_n \leqq a$

であることを数学的帰納法で示す。

　n = 0 のとき、 $a_0 = a , b_0 = b , a_1 = \dfrac{a+b}{2} , b_1 = \sqrt{ab}$ であり、いま $a > b$ であるから、明らかに、

$b < \frac{a+b}{2} , \sqrt{ab} < a$

であり、(1)の結果から $\dfrac{a+b}{2} < \sqrt{ab}$ であるから、

$b \leqq b < \frac{a+b}{2} < \sqrt{ab} <a \leqq a$

が成り立つ。すなわち(a)が成り立つことが示される。

　つぎに、n = k のときに(a)が成立すると仮定すると、

$b \leqq b_k < b_{k+1} < a_{k+1} < a_k \leqq a$

であり、 n = k + 1 のときを考えると、

$\begin{align*} a_{k+2} &= \frac{a_{k+1} + b_{k+1}}{2} < a_{k+1} \\ b_{k+2} &= \sqrt{a_{k+1} b_{k+1}} > b_{k+1} \end{align*}$

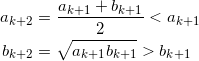
である。また、n = k の仮定より、 b ≦ b_k+1 , a_k+1 ≦ a だから、

$b \leqq b_{k+1} < b_{k+2} , \quad a_{k+2} < a_{k+1} \leqq a$

となる。最後に(1)の結果より、 $b_{k+2} < a_{k+2}$ であるから、

$b \leqq b_{k+1} < b_{k+2} < a_{k+2} < a_{k+1} \leqq a$

となる。以上より n = k + 1 のときにも(a)が成立。

　以上より、(a)は0以上のすべての整数 n について成立することが示された。

　さて、このことより、

数列 { a_n } は減少数列で下に有界であるから収束し、極限値 A をもつ。
数列 { b_n } は増加数列で上に有界であるから収束し、極限値 B をもつ。

　このとき、与えられた漸化式

$a_{n+1} = \frac{a_n+b_n}{2} , b_{n+1} = \sqrt{a_n b_n}$

であるから、極限を取ると、

$A = \frac{A+B}{2} , B = \sqrt{AB}$

であるから、これを解くと、A = B となる。よって { a_n } と { b_n } は同じ極限値 α に収束するといえる。

(3)

$\begin{align*} a_{n+2} &= \frac{a_{n+1}+b_{n+1}}{2} = \frac{\dfrac{a_n+b_n}{2} + \sqrt{a_n b_n}}{2} \\ &= \frac{a_n + b_n +2\sqrt{a_n b_n}}{4} = \bm{\frac{1}{4}(\sqrt{a_n} + \sqrt{b_n})^2} \end{align*}$

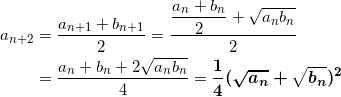
(4)　(3)と同様に、

$c_{n+2} = \frac{1}{4} (\sqrt{a_n} - \sqrt{b_n})^2$

であるから、(3)の結果と辺辺かけると、

$a_{n+2}c_{n+2} = \frac{1}{16}(a_n - b_n)^2$

すなわち

$c_{n+2} = \frac{1}{4a_{n+2}} c_{n+1}^2$

となる。
　よって、

$\frac{1}{2\sqrt{a_{n+2}}} < \frac{1}{2\sqrt{\alpha}}$

であれば問題の不等式を満たすことが示せるが、この式はすべての整数 i に対して $a_i > \alpha$ であることより成立する。
　以上より問題の式が成立することが示された。

解説

上界を持つ単調増加数列は収束する

　直感的に「増え続ける数列が収束するなんてことあるの？」と思う方もいるかもしれませんが、増加し続けるのに、ある数より小さくなければならないという条件がつくと、これはどこかの数字に収束せざるを得なくなります。これがざっくりとした説明です。

　この「壁」を上界や上限といった言葉で表現します。高校で学ばない表現なので説明をしておきましょう。
　上界とは「どの項よりも大きい（最大値が存在すれば、最大値と同じ数字でもよい）」ような数のことで、たとえば
　　a_n = 1 – 1n
とおくと、すべての a_n は 1 より小さいので、 1 や 2 や 1000 といった数字はこの数列の上界となります。もちろんすべての数列に上界が存在するとは限りません。
　上界が存在するとき、上界のうち最も小さい数、今の例でいえば 1 のことを、上限といいます。

　1つ例を上げてみましょう。初項 $\dfrac{1}{2}$ 、公比 $\dfrac{1}{2}$ の等比数列の和 S を考えてみましょう。

$S = \frac{1}{2} + \frac{1}{2^2} + \frac{1}{2^3} + \cdots$

　この和 S は、ある面積1の正方形の半分、次はその残りの半分、さらにその残りの半分、をどんどん足していくことをイメージします。半分ずつ足していくので確実にもとの面積 1 を超えることはありません（この1に近づいては行きそうですが）。このとき、 1 は上限を意味します。
　ところで、極限のところで学んだ通り、数列の公比が 1 より小さいので、この和 S は収束します。

　「上界を持つ単調増加数列の収束」の1つの例として、高校ではこれをベースに考えればよいでしょう。このことが、等比数列でなくとも成り立つ、ということです。どんどん”追いつめられていく”感じがつかめたでしょうか。

実は証明できない！

　「感覚はわかったけど、数学なんだから証明を書いてよ」とおっしゃる方もいるかもしれません。しかし、このことを証明することはできません。実はこの事実は「実数の連続性の公理」となっており、公理である以上証明することはできません。しかしそのことを高校の教科書では説明していません。詳しくは大学の解析学のテキストで勉強してみてください。

しかし高校数学でこのことを用いている

　そもそも高校で証明できないし、「有界な単調増加数列が収束する」という話も聞いたことがないぞ、というかたがほとんどでしょう。
　しかし、実は数学IIIの教科書には、このことが必ず載っているはずなのです。それは、自然対数 e を定義するところです。みなさん、お手元の数学IIIの教科書を引っ張ってきてみてください。