半径 1 の球に内接する正四面体の一辺の長さを求めよ。
[2005 北海道大・文理]
イズミの解答への道
基本的な問題をきちんと演習して解けるようにすることは、入試への近道といえます。この問題自体はどんな参考書にも載っている基本問題ですが、いざ出題されるとはたして?
解答
正四面体の一辺の長さを a とする。
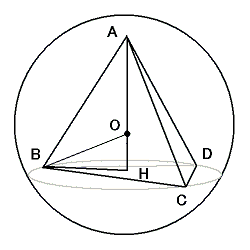
図のように正四面体 ABCD の A から底面 BCD に下ろした垂線の足を H 、円の中心を O とすると、
OA = OB = OC = OD = 1
である。
また、 点H は △BCD の外接円の中心であるから、正弦定理より、
![]()
より、
![]()
である(これは H が正三角形 BCD の重心と一致することからも分かる)。
ここで △ABH を取り出すと、三平方の定理より、
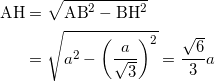
である。つぎに直角三角形 OBHにおいて三平方の定理より、
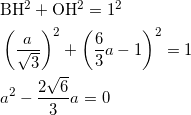
a > 0 より、 ![]() である。
である。
解説
等面四面体を使った別解
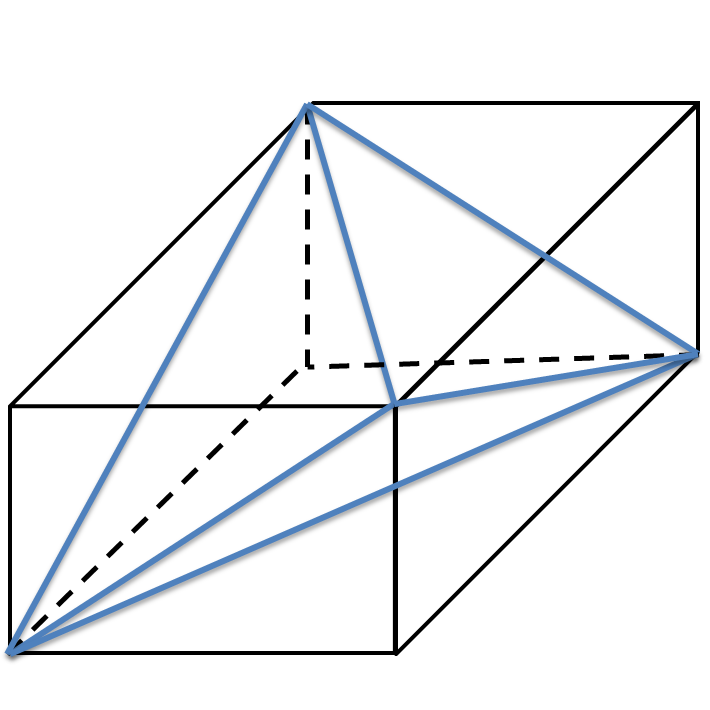
図のように立方体から、4つの三角錐 ABDE , BCDG , BEFG , DEGH を取り除いたものは正四面体となる。
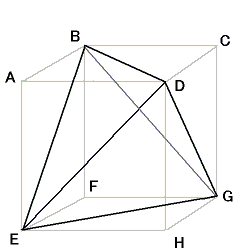
立方体の中心と円の中心は一致するので、立方体の一辺を a とすると、求める長さは、
![]()
である。また、中心から各頂点までの距離が 1 であることより、
![]() より
より ![]()
だから、求める長さは、
![]()
となる。
等面四面体は直方体から切り出す
上で紹介した別解の方法は、すべての四面体が合同である四面体(等面四面体)であるときに威力を発揮するものです。難関大においてはこのことを使うとうまく解くことができる問題がよく出題されていますので、確認しておくとよいでしょう。
四面体の中に球がある場合
さて、当面四面体のことは少し忘れて、この問題の派生型について考えてみましょう。
まず、今回の問題は球の半径が指定されている場合ですが、正四面体の一辺の長さが1であるときの外接球の半径を求める場合もあります。基本的には上記の方法の逆をたどれば求めることができるので、手を動かして計算してみてください。
また、今回は球の中に正四面体がある場合ですが、正四面体の中に球がある場合もあります。こちらは例題として扱っておきます。一緒に考えてみましょう。【解答1】、【解答2】それぞれに、覚えるべきポイントがあるので、2つの解答を載せておきます。
半径 1 の球に外接する正四面体の一辺の長さを求めよ。
解答1
球と四面体の面との接点は、四面体の面をなす正三角形の重心の位置である。
図のように球に外接する四面体A-BCDをおき、球の中心をP、△ABCと球が接する点をQ、△BCDと接する点をRとおき、辺BCの中点をMとおく。
また、求める正四面体の1辺の長さを a とする。
まず、球の半径は 1 だから、
PQ = PR = 1
であり、三平方の定理と重心の性質より、
![]()
であるから、
![]()
である。これらより、
![]()
となる。また、
![]()
である。
△AMR と △APQ は相似だから、
AR : MR = AQ : PQ
が成り立つので、
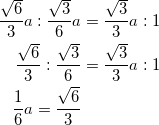
を解いて、![]() である。
である。
解答2
実は、内接球は、内接円の問題と同じように解くほうがよいでしょう。
コメント