正二十面体の体積［2016 順天堂大・医］

問題

　正二十面体の体積を求めてみよう。
　正二十面体の各面は正三角形であり、1つの頂点には5つの正三角形が集まっている。
　まず、Hを中心とする円に内接する正五角形ABCDEについて考える。
　ACとBEの交点をIとすると、△IABと△BCAを比較することにより、

$\text{AC} = \frac{\fbox{\hskip1em\rule{0pt}{1ex}} + \sqrt{\fbox{\hskip1em\rule{0pt}{1ex}} }}{\fbox{\hskip1em\rule{0pt}{1ex}}} \text{AB}$

となり、

$\cos \angle \text{BAC} = \frac{\fbox{\hskip1em\rule{0pt}{1ex}} + \sqrt{\fbox{\hskip1em\rule{0pt}{1ex}} }}{\fbox{\hskip1em\rule{0pt}{1ex}}}$

となることがわかる。これを用いて

$\text{AB} = \frac{ \sqrt{ \fbox{\hskip1em\rule{0pt}{1ex}}\fbox{\hskip1em\rule{0pt}{1ex}} - \fbox{\hskip1em\rule{0pt}{1ex}} \sqrt{\fbox{\hskip1em\rule{0pt}{1ex}} }}}{\fbox{\hskip1em\rule{0pt}{1ex}}} \text{AH}$

が求まる。

　次に、Hを通り円Hを含む平面に垂直な直線上に FA = AB となるようにFをとると、

$\text{FH} = \frac{\fbox{\hskip1em\rule{0pt}{1ex}}\fbox{\hskip1em\rule{0pt}{1ex}} + \sqrt{\fbox{\hskip1em\rule{0pt}{1ex}} }}{\fbox{\hskip1em\rule{0pt}{1ex}}} \text{AH}$

である。さらにFHの延長上に FO = AO となるように O をとると

$\text{HO} = \frac{\fbox{\hskip1em\rule{0pt}{1ex}}}{\fbox{\hskip1em\rule{0pt}{1ex}}} \text{AH}$

であり、

$\text{FO} = \frac{\sqrt{ \fbox{\hskip1em\rule{0pt}{1ex}}}}{\fbox{\hskip1em\rule{0pt}{1ex}}} \text{AH}$

となる。

　△FABの重心をGとすると、

$\text{FG} = \frac{\sqrt{ \fbox{\hskip1em\rule{0pt}{1ex}}}}{\fbox{\hskip1em\rule{0pt}{1ex}}} \text{AB} = \frac{ \sqrt{ \fbox{\hskip1em\rule{0pt}{1ex}}\fbox{\hskip1em\rule{0pt}{1ex}} - \fbox{\hskip1em\rule{0pt}{1ex}} \sqrt{\fbox{\hskip1em\rule{0pt}{1ex}} }}}{\fbox{\hskip1em\rule{0pt}{1ex}}} \text{AH}$

となる。

　このとき、正五角錐ABCDEFはOを中心とする急に内接する正二十面体の一部である。

$\text{GO} = \frac{\fbox{\hskip1em\rule{0pt}{1ex}} \sqrt{\fbox{\hskip1em\rule{0pt}{1ex}}} + \sqrt{\fbox{\hskip1em\rule{0pt}{1ex}}\fbox{\hskip1em\rule{0pt}{1ex}}}}{\fbox{\hskip1em\rule{0pt}{1ex}}\fbox{\hskip1em\rule{0pt}{1ex}}} \text{AB}$

となり、正二十面体の表面積は

$\fbox{\hskip1em\rule{0pt}{1ex}} \sqrt{\fbox{\hskip1em\rule{0pt}{1ex}}} \text{AB}^2$

となるので体積は

$\frac{\fbox{\hskip1em\rule{0pt}{1ex}}\fbox{\hskip1em\rule{0pt}{1ex}} + \fbox{\hskip1em\rule{0pt}{1ex}} \sqrt{\fbox{\hskip1em\rule{0pt}{1ex}}}}{\fbox{\hskip1em\rule{0pt}{1ex}}\fbox{\hskip1em\rule{0pt}{1ex}}} \text{AB}^3$

とあらわすことができる。

イズミの解答への道

　正二十面体の体積とは難しそう！と思いそうだが、誘導に従って解いていけば難しいところはない問題である。ただし、時間やミスが許されない医学部の入試において計算地獄の問題は厳しい。
　正二十面体が入試で出題されることはめったにないが、正二十面体の特殊な性質もあるので、解説でこれをまとめておこう。

解答

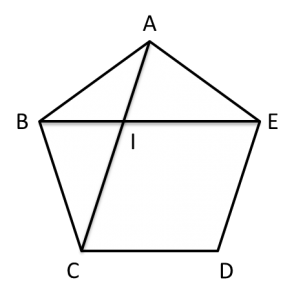
$2016_1$

　上の図のようにおいて、△ABI ∽ △ACBより
　　AB : AC = AI : AB
となる。ここで、IC = BC より、
　　AI = AC – IC = AC – AB
であるから、
　　AB² = AC ( AC – AB )
となり、ここで AC = x , AB = y とおくと、　　
　　x² – yx – y² = 0
より、

$x = \frac{y^2 \pm \sqrt{y^2 + 4y^2}}{2} = \frac{1 \pm \sqrt{5}}{2} y$