放物線と2接線のはさむ面積［2009 東工大］

問題

点Pから放物線 $\displaystyle y= \frac{1}{2}x^2$ へ2本の接線が引けるとき、2つの接点を A , B とし、線分PA , PB およびこの放物線で囲まれる図形の面積を S とする。 PA , PB が直交するときの S の最小値を求めよ。

［2009 東工大］

イズミの解答への道

　東工大の問題だが、1/6公式や放物線と2接線のはさむ面積の性質、相加相乗の利用など、学習すべきポイントがたくさん含まれる良問。解答中で使われている公式などについては、すべて使えるようにしておきたい。

解答

　 $\displaystyle f(x) = \frac{1}{2}x^2$ とすると、f’ ( x ) = x であるから、 x = t における接線は、

$\begin{align*} y &= f'(t) (x-t) + f(t) \\ &= tx - \frac{1}{2}t^2 \end{align*}$

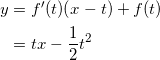
となる。よって、接点 A , B の x 座標を a , b ( a < b ) とすると、直線PA、PBを表す式は、
　　PA : $\displaystyle y = ax - \frac{1}{2}a^2$
　　PB : $\displaystyle y = bx - \frac{1}{2}b^2$
となる。これらは直交することから、
　　a・b = -1　　…(a)
また、このことから a , b の正負は互いに異なるので、 a < b としたことから、
　　a < 0 < b
であるといえる。

　いま、求める面積は、PA, PB の交点の x 座標を p とするとき、

$S = \int_a^p \left\{ \frac{1}{2} x^2 - \left( ax - \frac{1}{2} a^2 \right) \right\} dx + \int_p^b \left\{ \frac{1}{2} x^2 - \left( bx - \frac{1}{2} b^2 \right) \right\} dx$

で与えられる。これを計算して、

$\begin{align*} S &= \frac{1}{2} \times \frac{1}{6} \cdot \frac{1}{2}(b-a)^3 \\ &=\frac{1}{24}(b-a)^3 \end{align*}$

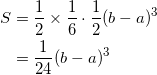
となる。（この式変形については解説を参考のこと。）

　ここで、(a)式より $\displaystyle a = -\frac{1}{b}$ を代入して、

$S = \frac{1}{24} \left( b + \frac{1}{b} \right)$

となる。ここで、 b > 0 より相加相乗の関係より、

$b+\frac{1}{b} \geqq \2 \sqrt{b \cdot \frac{1}{b}} = 2$

（等号は $\displaystyle b = \frac{1}{b}$ すなわち b = 1 のとき成立）が成り立つから、

$S \geqq \frac{1}{24} \cdot 2^3 = \frac{1}{3}$

となることより、最小値は $\displaystyle \bm{\frac{1}{3}}$ である。

解説

2次関数の2接線に関する特徴

　この問題の肝は「2次関数の2接線に関する特徴」です。それに加えて1/6公式と相加相乗と、高校数学の重要なテーマが目白押しで、どれも非常に重要なのでこの問題は必ず解けるようにしておきましょう。
　さて、まずは2次関数の2接線に関する性質をまとめておきます。

【公式】2次関数の2接線に関する性質

2次関数 y = f ( x ) = ax² + bx + c 上の2点 P ( p , f ( p ) ) , Q ( q , f ( q ) ) から引いた2接線は、
　　点 $\displaystyle \left( \frac{p+q}{2} , apq \right)$
で交わる

線分PQと2次関数で囲まれる面積 S₁ は、1/6公式を用いて、

$S_1 = \frac{|a|}{6}|p-q|^3$

である

S₁ と 2接線と2次関数で囲まれる面積 S₂ の間には、
　　S₁ : S₂ = 2 : 1
の関係がある

　これは、教科書には載っていませんが、受験のテクニックとしてはとても有名なもので、文章で覚えるのではなく、以下の図を使って丸暗記しておきましょう。

類題

　この問題は頻出問題です。次の問題も全く同じ解き方で解くことができます。誘導がある分易しいように見えますが、上記の「必殺技を示せ」という問題なので必殺技をそのまま使うわけには行かず、いちいちきちんと計算しないといけないので面倒くさいかもしれません。

放物線 C : y = x² + 2x 上の2点 ( a , a² + 2a ) , ( b , b² + 2b ) における接線をそれぞれ l_a , l_b とするとき、次の問いに答えよ。ただし a < b とする。 (1)　2直線 l_a , l_b の方程式を求めよ。また、 l_a と l_b の交点の x 座標を求めよ。
(2)　放物線 C と2直線 l_a , l_b とで囲まれた図形の面積 S を求めよ。
(3)　2直線 l_a , l_b が垂直に交わるように a , b が動くとき、 a , b が満たす関係式を求めよ。また、そのときの面積 S の最小値とそれを与える a, b の値を求めよ。

［2014 金沢大・文］