tanの値がすべて整数となる三角形［1984 一橋大］

三角形 ABC で tan A , tan B , tan C が整数のとき、その値を求めよ。［1984 一橋大］

イズミの解答への道

　いきなりこの問題が出題されると、手も足も出ない受験生が多い。ここで使える手法が、「一般性を失わない」ように条件を付加するというものである。
　いま、 ( tan A , tan B , tan C ) として ( 1 , 2 , 3 ) が解だとすれば、当然 ( 2 , 1 , 3 ) のようなものも解になる。そこで、始めから、 tan A ≦ tan B ≦ tan C という条件を仮定して求めてしまい、最後にこの条件を無くして他の解を得ればよい。
　実は、ヒント付きで同様の出題がされており、そちらも確認してもらいたい。

解答

　いま、 A ≦ B ≦ C と仮定すると、
　　　180°= A + B + C ≧ 3A
すなわち、
　　　（ 0 ≦ ） A ≦ 60°
であるから、
　　 $0 \leqq \tan \text{A} \leqq \sqrt{3}$
となる。 tan A は整数だから、 tan A = 1 となる。また、このとき三角形 ABC は鋭角三角形となる。
　さて、

$\begin{align*} \tan \text{A} &= \tan \{ 180^{\circ} - (\text{B} + \text{C} ) \} \\ &= - \tan ( \text{B} + \text{C} ) \\ &= - \frac{\tan \text{B} + \tan \text{C}}{1 - \tan \text{B} \tan \text{C}} = 1 \end{align*}$

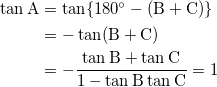
だから、これを整理して、
　　tan B tan C – tan B – tan C – 1 = 0
より、
　　( tan B – 1 ) ( tan C – 1 ) = 2
ここで、角B , C は鋭角だから、
　　tan B ≦ tan C
であり、tan B , tan C が整数であることも考えると、
　　( tan B , tan C ) = ( 2 , 3 )
となる。よって、
　　( tan A , tan B , tan C ) = ( 1 , 2 , 3 )
である。
　最後に A ≦ B ≦ C という条件がないとすれば、この順序をなくしたもの、すなわち、
　　{ tan A , tan B , tan C } = { 1 , 2 , 3 }
が解である。

解説

“一般性を失わない”

　この概念を理解し使いこなせるようになると、いよいよ上級者。一般性を失わない、ように条件を付加して問題を簡単にする手法を用いる問題を紹介しよう。

　x + y + z = xyz を満たす自然数の組 ( x , y , z ) を求めよ。

　この条件だけで解こうと手も足も出ない。しかし、この関係式は x と y が入れ替わっても同じ式となっている。つまり、はじめにこちらで x , y , z の大小関係を勝手に決めて解を求めてしまっても、あとでその関係性を外せばよいということである。
　たとえば、 ( x , y , z ) = ( 1 , 2 , 3 ) は題意を満たすが、この1つの解を求められれば、 x , y , z を自由に入れ替えることで、 ( x , y , z ) = ( 2 , 3 , 1 ) のような解もあることが自ずと分かる、ということである。

【解答】
　1 ≦ x ≦ y ≦ z としても一般性を失わない。この条件より、
　　3z ≧ xyz
すなわち、
　　3 ≧ xy
となるので、 x , y は ( x , y ) = ( 1 , 1 ) , ( 1 , 2 ) , ( 1 , 3 ) のいずれかである。

(i)　( x , y ) = ( 1 , 1 ) のとき
問題の式は
　1 + 1 + z = z
となるので、これを満たす z は存在しない。

(ii)　( x , y ) = ( 1 , 2 ) のとき
問題の式は
　1 + 2 + z = 2z
より、 z = 3 となり、 ( x , y , z ) = ( 1 , 2 , 3 ) が解となる。

(iii)　( x , y ) = ( 1 , 3 ) のとき
問題の式は
　1 + 3 + z = 3z
となるが、これを満たす自然数 z は存在しない。

　以上より、 ( x , y , z ) = ( 1 , 2 , 3 ) となる。

　問題には大小関係の制限はないので、その制限を取り払うと、求める解は、
　　( x , y , z ) = ( 1 , 2, 3) , ( 1 , 3, 2 ) , ( 2 , 1 , 3 ) , ( 2 , 3 , 1 ) , ( 3 , 1 , 2) , ( 3 , 2 , 1 )
となる。

類題

　まずは、上の問題とほとんど同じパターンで解くことができる問題です。

　鋭角三角形ABCの 3 つの内角をそれぞれ A , B , C で表し、 A ≦ B ≦ C とする。
(1)　tan A のとる値の範囲を求めよ。
(2)　tan C を tan A と tan B の式で表せ。
(3)　tan A , tan B , tan C がすべて整数のとき、 tan A , tan B , tan C の値を求めよ。

［2004 名城大・理工］

【解答】
(1)　A ≦ B ≦ C だから、
　　　180°= A + B + C ≧ 3A
　すなわち、A ≦ 60°となる。角 A は鋭角三角形の内角だから、 0 ≦ A ≦ 60°すなわち、
　　　tan 0°≦ tan A ≦ tan 60°
　　　0 ≦ tanA ≦ √3
(2)　tan ( 180°- θ) = – tanθを用いて、

$\begin{align*} \tan \text{C} &= \tan \{ 180^{\circ} - (\text{A} + \text{B} ) \} \\ &= - \tan ( \text{A} + \text{B} ) \\ &= - \frac{\tan \text{A} +\tan \text{B}}{1 - \tan \text{A} \tan \text{B}} \end{align*}$

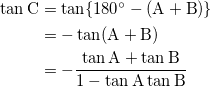
(3)　(1)の結果より、tan A = 1 となる。これを(2)に代入して、
　　(1 – tan B ) tan C = – ( 1 + tan B )
　　tan B tan C – tan C – tanB – 1 = 0
　　( tan B – 1 ) ( tan C – 1 ) = 2
となる。ここで、角B , C は鋭角だから、
　　tan B ≦ tan C
であるから、tan B , tan C が整数であることも考えると、
　　( tan B , tan C ) = ( 2 , 3 )
となる。以上より、
　　tan A = 1 , tan B = 2 , tan C = 3
である。