完全順列［2004 東工大（後）］

場所 1 から場所 n に異なる n 個のものが並んでいる。これらを並び替えてどれもが元の位置にならないようにする方法の総数を D ( n ) とする。ただし、 n ≧ 2 とする。
(1)　n = 4 の場合の並べ替え方をすべて書き出して、 D ( 4 ) を求めよ。
(2)　n ≧ 4 に対して
　　　D ( n ) = ( n – 1 ) { D ( n – 2 ) + D ( n – 1 ) }
　を証明せよ。

［2004 東工大（後）］

イズミの解答への道

　(1)では、もれなく書き出します。このときに、何に気付くかが(2)が解けるかどうかのポイントとなります。例えば 5 文字の並び替えを考えるときに、 4 文字の場合を上手く対応させたりできないか、ということを考えていきます。

　それを考えるために、さきに次の例題を見てみましょう。

　1 , 2 , 3 , 4 , 5 の順列 a₁ , a₂ , a₃ , a₄ , a₅ のうちで、
　　a₁ = 2 , a₂ ≠ 2 , a₃ ≠ 3 , a₄ ≠ 4 , a₅ ≠ 5
を全部満たすものは何通りあるか。また、
　　a₁ ≠ 1 , a₂ ≠ 2 , a₃ ≠ 3 , a₄ ≠ 4 , a₅ ≠ 5
を全部満たす物は何通りあるか。

［2002 東京農大］

【解答】
　1 から n （ n ≧ 2 ）の順列 a₁ , … , a_n のうち、 a_i ≠ i （ i = 1 , … , n ）を満たすものの個数を D ( n ) で表すとする。このとき、
　　D ( 2 ) = 1
　　D ( 3 ) = 2 （書き出せば、 231 , 312 より2つ）、
　　D ( 4 ) = 9 （書き出せば、 2143 , 2413 , 2341 , 3142 , 3412 , 3421 , 4123 , 4312 , 4321 ）
である。

（前半）
　1だけはどこにおいても構わないので、この 1 をポイントに次のように場合分けして考えます。

a₂ = 1 の場合
　このときは a₃ ≠ 3 , a₄ ≠ 4 , a₅ ≠ 5 を満たすことを考えればよく、これは D ( 3 ) = 2 通りである。
a₂ ≠ 1 の場合
　1 , 3 , 4 , 5 をそれぞれ、 a₂ , a₃ , a₄ , a₅ に並べてはいけない場合の数で（ a₂ に 1 を並べていけないというのは、冒頭の条件で決めたからです）、これは D ( 4 ) = 9 通りである。

　よって、 2 + 9 = 11 通り。

（後半）
　a₁ = 3 , a₁ = 4 , a₁ = 5 の場合もそれぞれ 11 通りなので、
　a₁ ≠ 1 , a₂ ≠ 2 , a₃ ≠ 3 , a₄ ≠ 4 , a₅ ≠ 5 を全部満たす物は D ( 5 ) = 44 通り。

　この問題でみたように、 a₁ = 2 とおいてみると、 1 をどこにおくかで2種類に場合分けができます。
　そのうち、 a₂ = 1 のように置いた場合には、残りの部分は数が減っただけでもともとの条件と同じことですから、簡単です。
　ポイントは a₂ ≠ 1 の場合です。これは条件を書き出すと、「 1 , 3 , 4 , 5 をそれぞれ、 a₂ , a₃ , a₄ , a₅ に並べてはいけない」ということになるのですが、この
「 1 , 3 , 4 , 5 をそれぞれ、 a₂ , a₃ , a₄ , a₅ に並べてはいけない」
と
「 2 , 3 , 4 , 5 をそれぞれ、 a₂ , a₃ , a₄ , a₅ に並べてはいけない」
は同じことであるというところに気付くところがポイントです。なぜなら、上の条件では 1 を a₂ に並べてはいけない、となっていますが、 1 を 2　と見なしても、どうせ問題の条件から 2 を a₂ に並べてはいけないからである。
　しかも、都合の良いことに下の条件を満たす場合の数は、 D ( 4 ) だとすぐに分かるので、もとの「 1 , 3 , 4 , 5 をそれぞれ、 a₂ , a₃ , a₄ , a₅ に並べてはいけない」という条件の場合の数もが D ( 4 ) だとわかります。
　この読み替えがうまくできれば、この問題は簡単に解くことができますが、一度経験していないとこれはなかなか難しいでしょう。

解答

(1)　以下、( 場所1 , 場所2 , 場所3 , … ) のように表す。
　はじめに 2 がくるものは ( 2 , 1 , 4 , 3 ) , ( 2 , 3 , 4 , 1 ) , ( 2 , 4 , 1 , 3 )
　はじめに 3 がくるものは ( 3 , 1 , 2 , 4 ) , ( 3 , 4 , 1 , 2 ) , ( 3 , 4 , 2 , 1 )
　はじめに 4 がくるものは ( 4 , 1 , 2 , 3 ) , ( 4 , 3 , 1 , 2 ) , ( 4 , 3 , 2 , 1 )
より、全部で 9 通り。

(2)　場所1に 2 を配置する場合を、次の2つの場合に分けて考える。

(i)　場所2に1が来る場合
　場所3から場所nには、3からnの n – 2 個の数字を、題意を満たすように配置しなければならず、その場合の数は、 D ( n – 2 ) である。

(ii)　場所2に1以外が来る場合
　「場所2から場所nに、1と3からnの合計 n – 1 個の数字を題意を満たすように配置するパターンのうち、場所2に1が入らない」（★）場合の数である。
　ところで、
「場所2から場所nに、2からnの n – 1 個の数字を題意を満たすように配置する」（★★）を考えると、★と★★は同じことを言っている。なぜなら、★には場所2に1が来ないという条件があるので、この数字1を数字2だとみなしても題意に反することが無い。

　★★の場合の数は、 D ( n – 1 ) であるから、(i)と(ii)より、場所1に2が来る場合の題意を満たす場合の数は、 D ( n – 1 ) + D ( n – 2 ) である。

　ところで、場所1に 3 , 4 , 5 , ……などの数字が来てもそれぞれの場合の数は同じく D ( n – 1 ) + D ( n – 2 ) となるため、題意を満たす場合の数 D ( n ) は、
　　D ( n ) = ( n – 1 ) { D ( n – 2 ) + D ( n – 1 ) }
となる。

研究

完全順列、モンモールの問題

　n人に当てた手紙を、n人の宛先を書いた封筒に「ランダムに」入れるとしましょう。すると、見事Aさんに送りたい手紙がAさん宛ての封筒に入るとは限りません。というより、外れることの方が多いような気がしませんか？　n が大きくなれば、ほとんど全部外れてしまうような気がします。
　この問題は、手紙がすべて違う人宛になってしまう場合の数を求める問題で完全順列（攪乱順列）とか、モンモールの問題と呼ばれ、モンモールが1708年に、n = 13 の場合の問題として提唱した。一般に n 人の場合はオイラーが解決した。その結果は本問で解いたとおり、
　　D ( n ) = ( n – 1 ) { D ( n – 2 ) + D ( n – 1 ) }
となる。

確率を求めよう

　では続いて、全ての手紙が間違った人に送られる確率を考えることにする。
　求める確率 P ( n ) は、
　　 $\displaystyle P ( n ) = \frac{D ( n )}{n!}$
で与えられる。
　　D ( n ) = ( n – 1 ) { D ( n – 2 ) + D ( n – 1 ) }
をこれに代入すると、

(a) 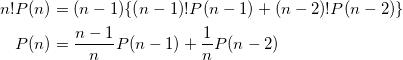$\begin{align*} n! P(n) &= (n-1) \{ (n-1)! P(n-1) + (n-2)! P(n-2) \} \\ P(n) &= \frac{n-1}{n} P(n-1) + \frac{1}{n} P(n-2) \end{align*}$

と変形でき、これは高校数学で学習する3項間漸化式である。

特性方程式
　　 $\displaystyle \alpha^2 = \frac{n-1}{n} \alpha + \frac{1}{n}$
を解いて、解が $\displaystyle \alpha = 1 , - \frac{1}{n}$ であることより、(a)式は、
　　 $\displaystyle P(n) - P(n-1) = -\frac{1}{n} \{ P(n-1) - P(n-2) \}$
と変形できる。数列 { P ( n ) – P ( n – 1) } は、
　　初項 $\displaystyle P ( 2 ) - P ( 1 ) = \frac{1}{2} - 0 = \frac{1}{2}$ （なぜなら、D ( 2 ) = 1 , D ( 1 ) = 0 )
　　公比 $\displaystyle - \frac{1}{n}$
の等比数列だから、

$\begin{align*} P(n) - P(n-1) &= \frac{(-1)}{n} \{ P(n-1) - P(n-2) \} \\ &=\frac{(-1)^2}{n(n-1)} \{ P (n-2) - P (n-3) \} \\ &= \cdots \\ &= \frac{(-1)^{n-2}}{n(n-1) \cdots 3} \{ P(2) - P(1) \} \\ &= \frac{(-1)^{n-2}}{n(n-1) \cdots 3} \times \left( \frac{1}{2} - 0 \right) \\ &= \frac{(-1)^n}{n!} \end{align*}$

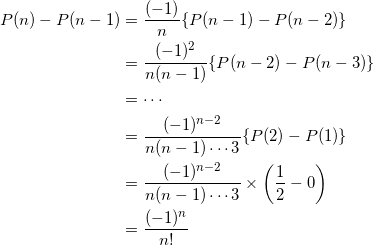
となるので、

$\begin{align*} P(n) &= \frac{(-1)^n}{n!} + P(n-1) \\ &=\frac{(-1)^n}{n!} + \frac{(-1)^{n-1}}{(n-1)!} +P(n-2) \\ &= \cdots \\ &= \frac{(-1)^n}{n!} + \frac{(-1)^{n-1}}{(n-1)!} + \cdots + \frac{(-1)^2}{2!} +P(1) \\ &=\sum_{k=2}^n \frac{(-1)^k}{k!} = \sum_{k=0}^n \frac{(-1)^k}{k!} \end{align*}$

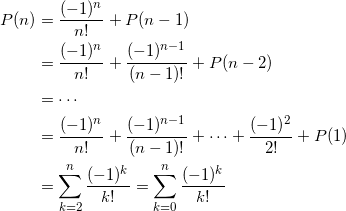
である。
　ここで、指数関数 e^x のテイラー展開（大学の微積の講義で学習する。詳しくは数学テキスト第9巻　極限と微分積分を参照）
　　 $\displaystyle e^x = 1 + \frac{1}{1!}x + \frac{1}{2!}x^2 + \frac{1}{3!}x^3 + \cdots = \sum_{k=0}^{\infty} \frac{1}{k!}x^k$
に、 x = -1 を代入して得られる式に等しいことから、
　　 $\displaystyle \lim_{n \to \infty } P(n) = e^{-1} = \frac{1}{e} = 0.37\cdots$
を得る。
　これは、 n が大きくなっても（すなわち人数が増えても）、全員の封筒を間違える確率は 37 ％程度に収束するということであり、この結果は直感とはやや違ったものである人も多いだろう。