次の積分の値を求めよ。
![]()
[2010 東京理科大・理・数学]
イズミの解答への道
積分計算にはいくつかのパターンがあり、 ![]() のパターンでは、 x = tanθ とおきかえるという定石はご存知のことでしょう。知らない人はきちんと勉強して下さい。
のパターンでは、 x = tanθ とおきかえるという定石はご存知のことでしょう。知らない人はきちんと勉強して下さい。
今回の問題は分母に1次式が含まれるパターンで、教科書では勉強しないかもしれませんが、うまく式変形して今回の定石に持ち込みます。一度は経験しておきたい問題です。
解答
![Rendered by QuickLaTeX.com \[ \int_0^1 \frac{2x+2}{x^2+x+1} dx = \underbrace{\int_0^1 \frac{2x+1}{x^2+x+1} dx}_A + \underbrace{\int_0^1 \frac{1}{x^2+x+1} dx}_B \]](http://izu-mix.com/math/wp-content/ql-cache/quicklatex.com-0d23120fe669399ca9f0a55f233590fc_l3.png)
とおいて、それぞれの積分を求める。
![Rendered by QuickLaTeX.com \begin{align*} A &= \int_0^1 \frac{2x+1}{x^2+x+1} dx \\ &=\left[ \log | x^2 + x + 1 | \right]_0^1 \\ &=\log 3 - \log 1 = \log 3 \end{align*}](http://izu-mix.com/math/wp-content/ql-cache/quicklatex.com-a679171af72cbc141d7fdc169e738305_l3.png)
となる。つぎに、
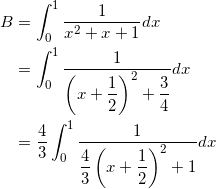
となることから、
![]()
とおくと、
![]()
であり、両辺の微分を取って、
![]()
となる。積分範囲は、
![Rendered by QuickLaTeX.com \[ \begin{array}{c|ccc} x & 0 & \to & 1 \\ \hline \tan t & \displaystyle \frac{1}{\sqrt{3}} & \to & \sqrt{3} \\ \hline t & \displaystyle \frac{\pi}{6} & \to & \displaystyle \frac{\pi}{3} \end{array} \]](http://izu-mix.com/math/wp-content/ql-cache/quicklatex.com-a5e6c269ea718ea2cff1f61ad4aa5000_l3.png)
となるので、求める積分は、
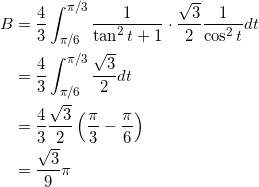
となる。以上より、求める積分の値は、
![]()

コメント