数学I・IIにまたがる分野です。
整数・証明・計算問題 1000以下の素数は250個以下である［2021 一橋大］
大学入試数学演習 ユークリッドの互除法［2018 首都大学東京・理・数理科］
大学入試数学演習 2015Cmが偶数になる最小のm ［2015 東京大・理］
大学入試数学演習 鳩の巣原理 ［2016 神戸大・理（後）］
整数・証明・計算問題 有理数・無理数の稠密性 ［2016 大阪大・専門数学］
大学入試数学演習 n進法で表される等式 ［2016 京都大・文］
大学入試数学演習 巡回群の直積と位数 ［2016 慶應大・理工］
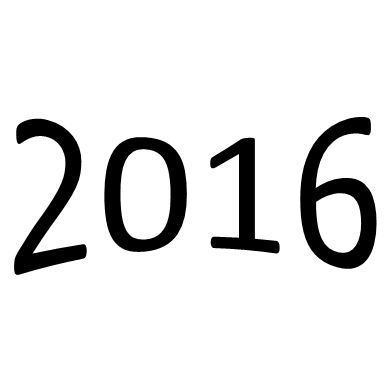大学入試数学演習 約数の個数と和 ［2016 慶應大・理工］
大学入試数学演習 tan1°は有理数か ［2006 京都大・共通（後）］
大学入試数学演習