巡回群の直積と位数［2016 慶應大・理工］

　iを虚数単位とする。次の事実がある。
　
【事実F】
　a , b を互いに素な正の整数とする。このとき、

$\left( \cos \frac{2a}{b}\pi + i \sin \frac{2a}{b}\pi \right)^k =\cos \frac{2}{b}\pi + i \sin \frac{2}{b}\pi$

となる整数 k が存在する。
　
(1)　等式

$\left( \cos \frac{4}{5}\pi + i \sin \frac{4}{5}\pi \right)^k =\cos \frac{2}{5}\pi + i \sin \frac{2}{5}\pi$

を満たす最小の正の整数 k は　　　である。

(2)　a , b を互いに素な正の整数とし、集合Pを、
　　P = { z | z は整数 k を用いて $\displaystyle \left( \cos \frac{2a}{b}\pi + i \sin \frac{2a}{b}\pi \right)^k$ と表される複素数 }
で定める。事実Fを考慮すると、集合Pの要素の個数 n(P) は　　　である。

(3)　事実Fを証明しなさい。

(4)　a₁ , b₁ を互いに素な正の整数とし、a₂ , b₂ も互いに素な正の整数とする。集合Q₁ , Q₂ を
　　Q₁ = { z | z は整数 k を用いて $\displaystyle \left( \cos \frac{2a_1}{b_1}\pi + i \sin \frac{2a_1}{b_1}\pi \right)^k$ と表される複素数 }
　　Q₂ = { z | z は整数 k を用いて $\displaystyle \left( \cos \frac{2a_2}{b_2}\pi + i \sin \frac{2a_2}{b_2}\pi \right)^k$ と表される複素数 }
で定め、集合Rを
　　R = { z | z は集合 Q₁ の要素と集合 Q₂ の要素の積で表される複素数 }
で定める。b₁ , b₂ が互いに素ならば、集合Rの要素の個数 n(R) は　　　である。b₁ , b₂ が互いに素でないとき、それらの最大公約数を d とすれば、集合Rの要素の個数 n(R) は　　　である。

［2016 慶應大・理工］

イズミの解答への道

　複素数とは不思議な数で、1のn乗根は特に興味深い数だと思いませんか。繰り返し掛けあわせることで巡回していき、大学で学ぶ群論の巡回群の例となっています。この問題のタイトルをわざと少し高尚なネーミングにしたのは、高校の数学が、大学の数学のすぐそばにあることを知っていただきたかったからです。

　ここで示されている「事実F」は、b乗根のうち、a番目の数を基準にしたとき、「“aとbが互いに素であれば、”k乗したときに、1番目の数にたどり着ける」ということを表しています。
　これを式で表すと、「どのような a に対しても ak ≡ 1 ( mod.b ) を見たす k が存在することを示せ」ということであり、さらに言い換えれば、
　　（※）a と b が互いに素なとき ak + bl = 1 を満たす k , l が存在する
ことを示せばよいのです。
　そして、この（※）の性質を「整数論の基本定理」と呼ぶことがあり、難関大学の大学入試でもたびたび出題される定理となっています。

　数論や群論のポイントとなる2つの内容を、複素数を通じて学ぶことができる興味深い問題だと思うのでピックアップしています。

解答

(1)　ド・モアブルの定理より、

$\cos \frac{4}{5}k\pi + i \sin \frac{4}{5}k\pi =\cos \frac{2}{5}\pi + i \sin \frac{2}{5}\pi$

であるから、偏角を比較して、

$\frac{4}{5}k\pi = \left( \frac{2}{5} + 2l \right) \pi$

を満たす正の整数 k , l を求めればよい。この式を変形して、
　　4k = 2 + 10l
　　2k – 5l = 1
となる。 k に小さい方から正の整数を代入して、 k = 3 , l = 1 のときが最小の k である。よって求める答えは k = 3 。

(2)　事実Fより、

$\left( \cos \frac{2a}{b}\pi + i \sin \frac{2a}{b}\pi \right)^{k_0} =\cos \frac{2}{b}\pi + i \sin \frac{2}{b}\pi$

を満たす k₀ が存在する。 k = nk₀ とおくと、ド・モアブルの定理より、

$\left( \cos \frac{2a}{b}\pi + i \sin \frac{2a}{b}\pi \right)^{k} =\cos \left( \frac{2}{b}\pi \times n \right) + i \sin \left( \frac{2}{b}\pi \times n \right)$

となる。この値は周期 b で繰り返し、 n = 0 , 1 , 2 , … , b – 1 の b 個の異なる値を取る。（このことは、複素数平面上に b 個の点をプロットすると、単位円上の正 b 角形の頂点となっていることから分かる。）
　よって、集合 P の要素は b 個ある。

(3)

$\left( \cos \frac{2a}{b}\pi + i \sin \frac{2a}{b}\pi \right)^k =\cos \frac{2}{b}\pi + i \sin \frac{2}{b}\pi$

となるためには、

$\frac{2ak}{b} \pi = \frac{2}{b} \pi + 2n\pi$

を満たす整数 k , n が存在する必要がある。式を変形して言い換えると、
　　ak – bn = 1
を満たす整数 k , n が存在することを示せばよい。
　
　いま、補題として、
「互いに素な整数 a , b に対して、 ak + bl = 1 を満たす整数 k , l が存在する」ことを示す。

　まず、
　　1a , 2a , 3a , … , ba
を b で割ったあまりはすべて異なる。
　なぜならば、2つの整数 i , j （ 1 ≦ i ≦ j ≦ b ) に対して、ia と ja を b で割った余りが等しいとすると、 ia – ja = ( i – j ) a が b の倍数でなければならないが、a と b は互いに素であるから ( i – j ) が b の倍数ということになるが、 i , j はいずれも b より小さいためこれもありえない。以上より、 i = j でなければならない。
　さて、 b 個の数 1a , 2a , 3a , … , ba を b で割ったあまりはすべて異なることから、この中に余りが 1 となるものが存在する。
それを ka とすると、
　　ka = ( -1 ) b + 1
を満たす整数 -l が存在することになる。以上より補題が示された。

　この補題を用いて、 l = -n とおけば、
　　ak – bn = 1
を満たす整数が存在することが示される。これにより、事実Fを示すことができる。

(4)　(2)でみたように、事実Fを用いると、
　　Q₁ = { z | z は整数 k を用いて $\displaystyle \left( \cos \frac{2}{b_1}\pi + i \sin \frac{2}{b_1}\pi \right)^k$ と表される複素数 }
　　Q₂ = { z | z は整数 k を用いて $\displaystyle \left( \cos \frac{2}{b_2}\pi + i \sin \frac{2}{b_2}\pi \right)^k$ と表される複素数 }
となるので、Rの要素としては、

$\begin{align*} &\left( \cos \frac{2}{b_1}\pi + i \sin \frac{2}{b_1}\pi \right)^{k_1} \left( \cos \frac{2}{b_2}\pi + i \sin \frac{2}{b_2}\pi \right)^{k_2} \\ &=\left( \cos \frac{2 k_1}{b_1}\pi + i \sin \frac{2 k_1}{b_1}\pi \right) \left( \cos \frac{2 k_2}{b_2}\pi + i \sin \frac{2 k_2}{b_2}\pi \right) \\ &=\cos \left( \frac{2 k_1}{b_1} + \frac{2 k_2}{b_2} \right) \pi + i \sin \left( \frac{2 k_1}{b_1} + \frac{2k_2}{b_2}\pi \right) \\ &=\cos \frac{2(k_1 b_2+k_2 b_1)}{b_1 b_2} \pi + i \sin \frac{2(k_1 b_2+ k_2 b_1)}{b_1 b_2} \pi \\ &=\left( \cos \frac{2}{b_1 b_2} \pi + i \sin \frac{2}{b_1 b_2} \pi \right)^{k_1 b_2 + k_2 b_1} \end{align*}$

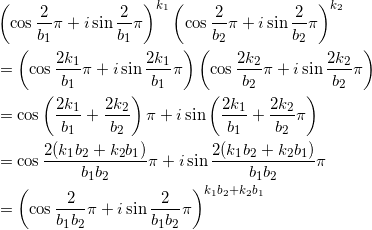
　ここで、(3)の補題より、
　　「互いに素な整数 b₁ , b₂ に対して、 kb₁ + lb₂ = 1 を満たす整数 k , l が存在する」
ので、 nk = k₂ , nl = k₁ と置き直すことで、
　　「互いに素な整数 b₁ , b₂ に対して、 k₂b₁ + k₁b₂ = n を満たす整数 k , l が存在する」
すなわち、
　　「互いに素な整数 b₁ , b₂ に対して、 k₁b₂ + k₂b₁ はすべての整数を取る」
ことがいえる。よって、 b₁ , b₂ が互いに素であれば、(2)と同様に、 $\displaystyle \left( \cos \frac{2}{b_1 b_2} \pi + i \sin \frac{2}{b_1 b_2} \pi \right)^{k_1 b_2 + k_2 b_1}$ は n ( R ) = b₁b₂ 個の値を取る。

　つぎに、 b₁ , b₂ が互いに素でないとき、その最大公約数が d であれば、互いに素な整数 b₁‘ , b₂‘ を用いて、
　　b₁ = db’₁
　　b₂ = db’₂
と表せるので、
　　k₁b₂ + k₂b₁
　　= d ( k₂b’₁ + k₁b’₂ ) = dn
となることより、 k₁b₂ + k₂b₁ はすべての d の倍数を表すことがいえる。
　よって、このときRの要素としては、

$\left( \cos \frac{2}{b_1 b_2} \pi + i \sin \frac{2}{b_1 b_2} \pi \right)^{dn} =\left( \cos \frac{2}{\displaystyle \frac{b_1 b_2}{d}} \pi + i \sin \frac{2}{\displaystyle \frac{b_1 b_2}{d}} \pi \right)^{n}$

となるので、 n ( R ) = $\displaystyle \bm{ \frac{b_1 b_2}{d} }$ 個の値を取る。

解説

(4)を分かりやすく考える

　次のような問題を考えてみよう。

　2つのボタンA、Bが繋がれたアナログ時計がある。初期段階ではアナログ時計は0時を指しており、以下では分のことは考えなくてよい。
(1) Aのボタンを押すと時計の針は3時間進み、Bのボタンを押すと時計の針は4時間進む。このとき、これらのボタンを適当な回数押すことで、この時計は1時から12時までのすべてを指し示す事ができることを示せ。
(2) Aのボタンを押すと時計の針は2時間進み、Bのボタンを押すと時計の針は6時間進む。このとき、これらのボタンを適当な回数押しても、この時計は1時から12時までのすべてを指し示すことはできないことを示せ。（指し示せない時刻があることを示せ。）

　簡単に解答を書いておこう。どちらも0時はボタンを押さずに示すことができる。(1)では、Aのボタンだけで、3時、6時、9時が示せる。次にBのボタンを1度押したあと、Aのボタンを繰り返し押せば、4時、7時、10時、1時を示せる。Bのボタンを2度押したあと、Aのボタンを繰り返し押せば、8時、11時、2時、5時を示せる。以上より、すべての時間を指し示せることが示された。一方、(2)では明らかに奇数の時間は示せない。（示せるのは偶数時間の6種類だけである。）

　なぜこのような差が生まれるかというと、(1)ではボタンで進む時間が“互いに素”であり、(2)では“互いに素になっていない”ことがポイントである。12を周期とする巡回について、互いに素であれば、12種類すべてが現れるが、最大公約数が2の2つの巡回を組み合わせると、現れる数字は最大公約数の2で割った、6種類に半減する事がわかる。