円周率が3.05より大きいことの証明［2003 東京大・理］

　円周率が3.05より大きいことを証明せよ。

［2003 東京大・理］

イズミの解答への道

　そもそも円周率とはなんだったか？　という定義を知らないと書き出しから困ります。解答には円周率の定義を書くことも必要となります。そして、定義に基づいて円周率を近似的に求めていくのですが、これは教科書だけ勉強していたのではなかなか思いつかないでしょう。

解答

　円周率は、「円周の直径に対する比の値」と定義される。すなわち、単位円（直径 2 ）の円周の長さは 2π である。

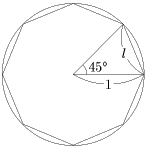
　 $tokyo_2003_01$

　さて、図のように半径 1 の円に内接する正八角形を考えるとき、一辺の長さを l とすると、円周は正八角形の周より長いので、
　　8l < 2π　…(a)
が成り立つ。両辺は正であるから、(a)は両辺を2乗した、
　　16l² < π²　…(a)’
と同値である。また、示したいのは 3.05 < π であるから、　　3.05² ≦ 16l²　…(b)
が証明すれば良い。

　いま、
　　3.05² = 9.3025
であり、余弦定理より、

$\begin{align*} l^2 &= 1^2 + 1^2 -2\cdot 1 \cdot 1 \cdot \cos 45^{\circ} \\ &=2 -\sqrt{2} \end{align*}$

であるから、(b)式は、

(c) 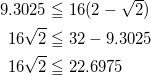$\begin{align*} 9.3025 &\leqq 16( 2- \sqrt{2}) \\ 16\sqrt{2} &\leqq 32 - 9.3025 \\ 16\sqrt{2} &\leqq 22.6975 \end{align*}$

と同値である。すなわち(c)式が示せれば良い。
　いま、
　　1.415² = 2.002225
であるから、
　　√2 < 1.415
であるから、

$16\sqrt{2} < 16 \times 1.415 = 22.64$

となり、(c)式は成立する。
　以上より、円周率が3.05より大きいことが示された。

解説

先見の明？

　実は、2001年の岐阜大で次のような問題が出題されている。

　円周率πの値の数値を知らないものとして、図形と計算を用いてπが不等式 3 ＜ π ＜ 10/3 を満たすことを示せ。

［2001 岐阜大・教育（後）］

　この問題でも、基本的には行うことは同じです。 3 < π を示すのは今回と同様に正八角形を内接させます。近似計算がこれよりは楽です。 $\displaystyle \pi < \frac{10}{3}$ も同様に、正八角形を外接させればよいでしょう。
　もう少し誘導の多い問題が、2001年の高知大・理で出題されている。

　単位円に内接する正 n 角形の周の長さをS_n、外接する正 n 角形の周の長さを T_n で表すと、
　　　S_n < π < T_n
である。次の問に答えよ。
(1)　S_n、T_n を n で表し、{ S_n }、{ T_n }はともに 2π に収束することを示せ。
(2)　S_n、T_n に対して、

$\begin{align*} T_{2n} &= \frac{2S_n T_n}{S_n + T_n} \\ S_{2n} &= \sqrt{S_nT_{2n}} \end{align*}$

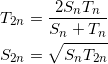
が成り立つことを示せ。
(3)　(2)を用いて、S₁₂、T₁₂の値を求めよ。
(4)　(3)を用いて、不等式
　　　3.10 < π < 3.22
を示せ。必要ならば、
　　　1.414 < $\sqrt{2}$ < 1.415
　　　1.732 < $\sqrt{3}$ < 1.733
　　　2.449 < $\sqrt{6}$ < 2.450
を用いよ。

［2001 高知大・理］

　高知大の問題ではすでにルートの値が与えられているのですが、東京大・岐阜大の問題では、 $\sqrt{2}$ などの値の取り扱い（数値の評価）も重要で、上手に説明した解答を書くためには、ある程度の解答の推敲が必要かもしれません。

　なお、数値の評価が必要な問題としては、過去に以下のような出題がある。参考にしてもらいたい。

京都大の不等式の評価
定積分と不等式の評価［1999 東京大・理］

円周率π

　πの近似値は、古来から多数考えられており、アルキメデスは正96角形を円に内接させ、

$3\frac{10}{71} < \pi < 3\frac{1}{7}$

　　　
を示したといわれている。分数を小数に直すと、3.1408 < π < 3.1428です。およそ 3 でいいという一昔前の教育課程からしてみれば、これでも十分良い近似である。　実用的な近似分数としては、一つは上に登場した $\displaystyle 3 \frac{1}{7} = \frac{22}{7}$ があげられる。7と22が円周率の近似値に使われていることから、7月22日は円周率近似値の日となっているそうだ。
　その他にも、113355 と数字が覚えやすくより円周率に近い $\displaystyle \frac{355}{113}$ などがある。

漸化式で円周率を求める

　単位円に内接する正 6×2² 角形を描き、一辺の長さを a_n とすると、

$a_{n+1} = \sqrt{2 - \sqrt{4-a_n^2}}$

という漸化式が成り立つことが、ピタゴラスの定理などを用いて示せる（証明は後述）。

　正 6×2² 角形の周の長さは 6×2ⁿ×a_n であり、円周は 2π となるので、

$\lim_{n \to \infty} (3 \times 2^n \times a_n ) = \pi$

となることが分かる。これは、 n = 0 のとき正六角形で、a₀ = 1 であり、ここから順次 a_n を求めることでπの近似値を求めることができる。

　最後に、冒頭の漸化式を証明しておこう。（省略）

ライプニッツの公式

マチンの公式

　マチン（J.machin, 1680-1751）は、πの値を与える四季を見つけた。それは、

という式である。このマチンの公式に関する問題が、2001年の熊本大で出題されているので簡単に紹介する。（省略）

ウォリスの公式

ゼータ関数

　ゼータ関数とは、

$\zeta(s) = \sum_{n=1}^{\infty} \frac{1}{n^s}$

で表される関数である。 s は複素数全体を動く数を考えるもので、整数論だけでなく複素関数論や、物理学でも広く利用される関数でありながら、現在も未だ未解決の問題をもつ謎の多い関数である。
　s が小さい偶数のときについてはその結果もすでに分かっており、たとえば

$\sum_{n=1}^{\infty} \frac{1}{n^2} = 1 + \frac{1}{2^2} + \frac{1}{3^2} + \frac{1}{4^2} + \cdots = \frac{\pi^2}{6}$

などは有名である。

円周率の暗記法

　英語では単語の綴り文字数を対応させて、次のような覚え方が有名だそうです。

Yes, I have a number. (3.1416)
May I tell a story purposing to render clear the ratio circular perimeter breadth, revealing one of the problems most famous in modern days, and the greatest man of science anciently known. (3.1415926535897932384626433832795)

　2つ目の英文の訳は次の通り。「円周と直径の比を明らかにする話をさせてください。それは今日もっともよく知られた問題のひとつで、古代、もっとも偉大な科学者には知られていたものです。」