問題
以下の問いに答えよ。
(1) 実数 a に対し、2次の正方行列 A , P , Q が、5つの条件
A = aP + ( a + 1 ) Q , P2 = P , Q2 = Q , PQ = O , QP = O
をみたすとする。ただし 
である。このとき、
( P + Q ) A = A
が成り立つことを示せ。
(2) a は正の数として、行列 
を考える。この A に対し、(1)の5つの条件をすべて満たす行列 P , Q を求めよ。
(3) n を 2 以上の整数とし、 2 ≦ k ≦ n を満たす整数 k に対して、
とおく。行列の積
AnAn-1An-2…A2
を求めよ。
イズミの解答への道
問題自体は誘導に従って解いていけばよいので、難しいところはほとんど無い。(3)では(1)をヒントにこの P , Q の有用性を理解していればよい。これはテーマを知っているとよりスムーズだっただろう。
本問のテーマは行列のスペクトル分解。詳しくは大学の線型代数などで学習するものなので、高校で理論立てて学ぶ機会はないですが、受験レベルの参考書であれば類題が1題は紹介されている問題でもあるので、慣れておくとよいでしょう。
解答
(1)で与えられた条件を順に(a)?(e)とする。
(1) 条件式に(a)を代入すると、
（左辺） = ( P + Q ) { aP + ( a + 1 ) Q }
= aP2 + ( a + 1 ) PQ + a QP + ( a + 1 ) Q2
ここで条件(b)?(e)を代入すると
= aP + ( a + 1 ) Q = A
となることから、題意は示された。
(2) a は正の数より、 A の行列式
det A = a ( a + 1 ) ≠ 0
であることから A には逆行列が存在し、
( P + Q ) A = A
の右から A-1 をかけて
P + Q = E
となる（ただし E は2次の単位行列）。
P + Q = E … (f)
aP + ( a + 1 ) Q = A … (g)
として(f)と(g)を連立して、 P , Q について解くと、
![\[ P = \begin{pmatrix} 1 & 0 \\ -1 & 0 \end{pmatrix} , Q = \begin{pmatrix} 0 & 0 \\ 1 & 1 \end{pmatrix} \]](http://izu-mix.com/math/wp-content/ql-cache/quicklatex.com-d9fed507c94aafbdfd5717f38f8840b5_l3.png "Rendered by QuickLaTeX.com")
となる。このとき確かに条件を満たすことからこれが答えである。
(3) いま、適当な k , l , m , n について、条件(b)?(e)を用いることで、
( kP + lQ ) ( mP + nQ) = kmP2 + knPQ + lmQP + lnQ2
= kmP + lnQ
となる（すなわち、xP + yQ の形のものを掛けたとき、その答えはそれぞれの P の係数を掛け合わせたものに P を掛けたものと、それぞれの Q の係数を掛け合わせたものに Q を掛けたものの和になる）。いま、
Ak = kP + ( k +1 ) Q
であるから、
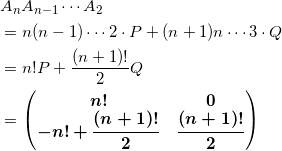
となる。
解説
スペクトル分解
ある行列 A を、 A に対して決まる行列 P , Q を用いて
A = αP + βQ
と表すことを行列 A のスペクトル分解という。この P と Q の性質、定め方が重要であり、P , Q は本問でも条件として課されていた条件
P2 = P , Q2 = Q , PQ = O , QP = O
を満たさなければならない。 P , Q の性質、定め方については後述するとして、このスペクトル分解の重要な理由は、
An = ( αP + βQ )n
= ( αP )n + ( βQ )n ← PQ = QP = O を用いた
= αnPn + βnQn
= αnP + βnQ ← Pn = P , Qn = Q を用いた
となり、 n 乗計算が楽になるということにある。
コメント