四面体ABCDは、4つの面のどれも3辺の長さが 7 , 8 , 9 の三角形である。この四面体のABCDの体積は である。
[2014 早稲田大・教育]
イズミの解答への道
「4つの面が合同な四面体は、直方体から切り出して作ることができる」という考え方を知っているかどうか、という問題です。これを知らないとこの問題を解くのには時間がかかってしまいます。
解説では、この性質を利用することで見通しが良くなる難関大の出題をいくつか紹介します。
解答
図のような直方体を考えると、その中に問題に与えられた四面体 ABCD を配置することができる。
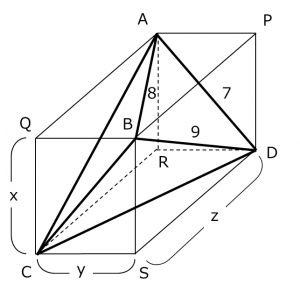
求める体積を V とする。これは、直方体から四面体が関係しない4つの部分を切り取ったものである。
いま、四面体BCSDの体積を V’ とすると、
![]()
であり、残り3つの四面体も同じ体積である。よって、求める体積Vは、
![]()
である。
次に、三平方の定理より、
x2 + y2 = 72 = 49 …(a)
y2 + z2 = 82 = 64 …(b)
z2 + x2 = 92 = 81 …(c)
を、x2, y2, z2 について解くと、
(3つの式を辺辺足して2で割ったものは
x2 + y2 + z2 = 97 …(d)
となり、 (d) – (b) より、)
x2 = 33
同様に、
y2 = 16
z2 = 48
となるから、
![]()
となるので、求める体積は、
![]()
となる。
解説
等面四面体
4つの面が合同な四面体のことを等面四面体といい、高校では特別取り上げるテーマではありませんが、受験数学では頻出のテーマとなっています。
なぜこの四面体がよく取り上げられるかというと、上記で示したように「直方体から切り出す」という特殊な方法があり、これを思いつけるかどうかを問うことが多いからです。事実、これを知らないと解くのが難しくなってしまいます。
以下では、等面四面体にまつわる出題を幾つか紹介します。どれも難関大での出題であり、この「直方体から切り出す」というのがポイントになっていることがわかるでしょう。
類題1
まずは上記とほぼ同じで、等面四面体の体積を求める問題です。(2)は数学IIIの知識が入りますが、問題を見たときに等面四面体だと見抜く目を養うためにも、このような例題を紹介しておきます。
![]() を満たす実数θに対し、xyz空間内の4点 A ( cosθ, cosθ, sinθ ) , B ( -cosθ, -cosθ, sinθ ) , C ( cosθ, -cosθ, -sinθ ) , D ( -cosθ, cosθ, -sinθ ) を頂点とする四面体の体積を V ( θ ) とする。このとき以下の各問いに答えよ。
を満たす実数θに対し、xyz空間内の4点 A ( cosθ, cosθ, sinθ ) , B ( -cosθ, -cosθ, sinθ ) , C ( cosθ, -cosθ, -sinθ ) , D ( -cosθ, cosθ, -sinθ ) を頂点とする四面体の体積を V ( θ ) とする。このとき以下の各問いに答えよ。
(1) ![]() を求めよ。
を求めよ。
(2) ![]() における V ( θ ) の最大値を求めよ。
における V ( θ ) の最大値を求めよ。
[2014 東京医科歯科大(一部)]
【解答】
図を書いてみると分かりますが、これも3辺の長さが 2sinθ, 2cosθ, 2cosθ の直方体から四隅を除いたものになるので、 V ( θ ) を直接求めると、
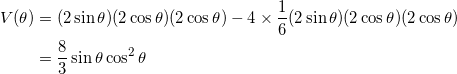
となるので、
(1) ![]()
(2) ![]() より、
より、
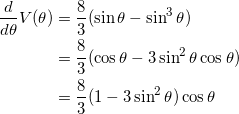
であるから、![]() の範囲において、
の範囲において、 ![]() を満たすθをθ = α とおくと、次の増減表を得る。
を満たすθをθ = α とおくと、次の増減表を得る。
![Rendered by QuickLaTeX.com \[ \begin{array}{|c||c|c|c|c|c|} \hline \theta & 0 & \cdots & \alpha & \cdots &\displaystyle \frac{\pi}{2} \\ \hline \displaystyle \frac{dV(\theta)}{d\theta} & & + & 0 & - & \\ \hline V(\theta) & & \nearrow & & \searrow & \\ \hline \end{array} \]](http://izu-mix.com/math/wp-content/ql-cache/quicklatex.com-414ecc1bc18e4e9b23e7f56d1231ae40_l3.png)
以上より、V ( θ ) は θ = α で最大値
![Rendered by QuickLaTeX.com \[ V(\alpha) = \frac{8}{3} \left\{ 1 - \left( \frac{1}{\sqrt{3}} \right)^2 \right\} \cdot \frac{1}{\sqrt{3}} = \bm{\frac{16\sqrt{3}}{27}} \]](http://izu-mix.com/math/wp-content/ql-cache/quicklatex.com-cc178eda5e76577416d4416740ecfeb6_l3.png)
をとる。
類題2
ここからは少し難しくなります。この問題は、
- 自分で座標を設定する
でも紹介しますが、「等面四面体が直方体から切り出せる」ことを知っていれば、この問題もこの事実を利用して解けないかと考えることで、以下の解答が思いつきます。
△ABCは鋭角三角形とする。このとき、各面すべてが△ABCと合同な四面体が存在することを示せ.
[1999 京都大・理(後)]
【解答】
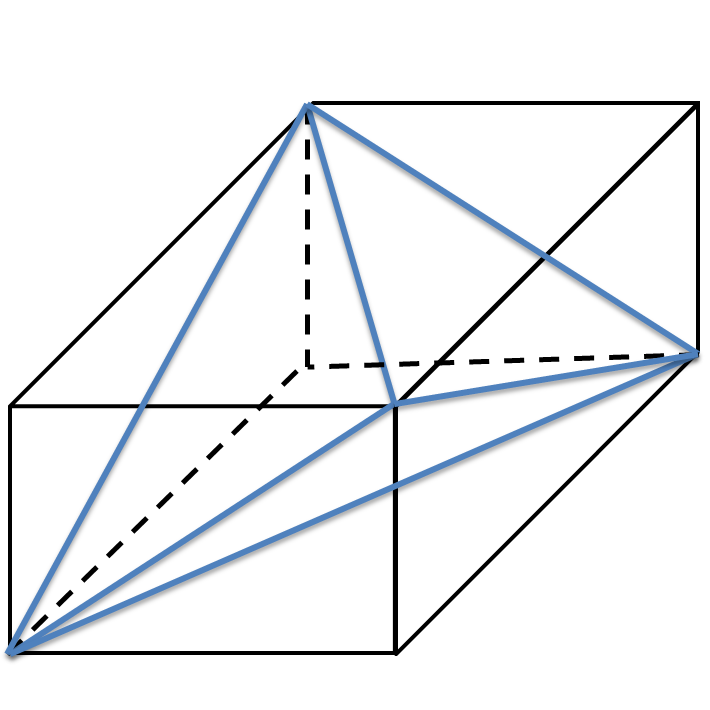
コメント