問題
(1) k , n を正の整数とし、
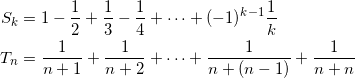
とする。このとき、等式 Sk = Tn が成立する k を n で表せ。またその等式を n に関する数学的帰納法によって証明せよ。
(2) n を正の整数とするとき、 Sn の最大値と最小値を求め、解答欄にそれらの値を記入せよ。また、その理由を示せ。
イズミの解答への道
(1)は予想して帰納法で証明、という最も基本的なパターンですが、帰納法で n = k + 1 のときを示す際の式変形に多少苦労するかもしれません。
(2)ではまず解答を書く前に与えられた式から Si の大小関係をつかみましょう。答えが分かったあとで、その道筋をうまく式から導けるように考えるとよいでしょう。
解答
書き出していくと、
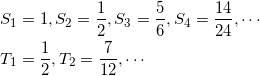
となることから、
S2n = Tn ……(※)
すなわち、 k = 2n と考えられる。次に(※)を数学的帰納法によって証明する。
(i) n = 1 のとき
上で調べたとおり、 S2 = T1 より、成立。
(ii) n = k のときに成立すると仮定すると、 n = k + 1 のとき、
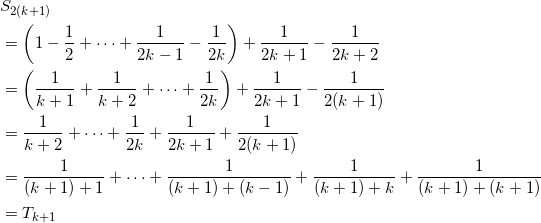
となることより成立。
よって数学的帰納法によって題意は示された。
(2) 問題文に与えられた Sk , Tn の式を (a) , (b) とする。
まず、(b)より、明らかに、
![]()
すなわち、
(c) ![]()
である。また、 Sn の式から、
![]()
となることから、
(d) ![]()
が成り立つ。また、(a)式から、
![]()
であるから、
(e) ![]()
である。
(c) , (d) より最大値は S1 あるいは S2n のどちらかであるが、(d) と (e) より、
![]()
となるから最大値は S1 である。
同様に最小値は S2 あるいは S2n-1 のどちらかであるが、(c) と (e) より、
![]()
であるから、最小値は S2 である。
よって、最大値は ![]() 、最小値は
、最小値は![]() となる。
となる。
研究
k = 2n のときだけ?
(1)の証明では、 k = 2n のとき“のみ”であることは証明できていない。しかし、実際に(2)で現れた (c) , (d) , (e) 式から、 i ≠ j に対して Si ≠ Sj となる( Sk が2回同じ値をとることはない))ことが示されるので、 k = 2n のときのみであることを示すことはできる。
このことまでを解答として求めると難しいということもあってか、(1)ではここを問題の対象としていない。また、次に示す例題ではその問題が起こらないように配慮されている。
類題1
実はこの等式は非常に有名で、類題も多数ある。1つ目は(1)とほぼ同じ問題である。
正の整数 n に対して
![Rendered by QuickLaTeX.com \[ S(n) = \sum_{p=1}^{2n} \frac{(-1)^{p-1}}{p} , \quad T(n) = \sum_{q=1}^n \frac{1}{n+q} \]](http://izu-mix.com/math/wp-content/ql-cache/quicklatex.com-103636dfefbee37715fbc0b5aaed333e_l3.png)
とおく。等式 S ( n ) = T ( n ) ( n = 1 , 2 , 3 , …… )が成り立つことを、数学的帰納法を用いて示せ。
[2005 大阪大・理]
【解答】
(1)と同じなので省略。
類題2
次の類題は数学IIIの知識を必要とする。結果としてある有名な無限級数の和を求めることができる。これがこの等式がよく出題される理由でもある。
自然数 n に対し、
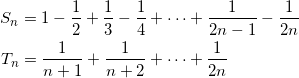
とおく。このとき、次の問いに答えよ。
(1) Sn = Tn ( n = 1 , 2 , …… )となることを証明せよ。
(2) 次の不等式が成り立つことを示せ。
![]()
(3) ![]() を求めよ。
を求めよ。
[2001 大阪女子大・理(後)]
【解答】
(1) 省略。
(2) ![]() とおいて区分求積法に寄って積分を近似する。ここで、 f ( x ) は単調減少だから、
とおいて区分求積法に寄って積分を近似する。ここで、 f ( x ) は単調減少だから、
![]()
なので、
![Rendered by QuickLaTeX.com \[ \sum_{k=1}^n \frac{1}{n} f \left( \frac{k}{n} \right) < \int_0^1 \frac{dx}{1+x} < \sum_{k=0}^{n-1} \frac{1}{n} f \left( \frac{k}{n} \right) \]](http://izu-mix.com/math/wp-content/ql-cache/quicklatex.com-e87b3a05ae7890e7972c58a876741e83_l3.png)
が成り立つ。左辺は Tn に等しく、右辺は、
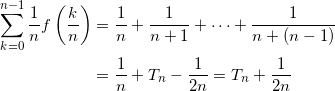
となることから、与えられた式は示される。
(3) (2)の結果と、 Sn = Tn より、
![]()
であり、 n → ∞ のとき、はさみうちの定理より、
![]()
となる。
類題3
例題2と同じですね。ダメ押しです。
![Rendered by QuickLaTeX.com \[ \sum_{i=1}^n \frac{1}{n+i} + \sum_{j=1}^{2n} \frac{(-1)^j}{j} = 0 \]](http://izu-mix.com/math/wp-content/ql-cache/quicklatex.com-08938b4b895431109aafdc8e3284cf7a_l3.png)
が成り立つことを数学的帰納法を用いて証明せよ。
(2) 等式
![Rendered by QuickLaTeX.com \[ \sum_{j=1}^{\infty} \frac{(-1)^j}{j} = -\log 2 \]](http://izu-mix.com/math/wp-content/ql-cache/quicklatex.com-46b72ab2e43dafbccb7fcabb00059a79_l3.png)
が成り立つことを証明せよ。
【解答】
例題2を利用して、考えてみてください。(1)の結果を使い、![]() が
が![]() と関連するところまでを見通せますか?
と関連するところまでを見通せますか?

コメント