問題
3辺の長さが 5 , 12 , 13 である三角形において、長さが 12 , 13 である2辺によってはさまれる角の大きさをθとする。このとき n°< θ < ( n + 1 )°となる整数 n は である。
イズミの解答への道
三平方の定理を学んだ中学生のときからお馴染みの 5 , 12 , 13 の直角三角形の最鋭角の角度θは大体何度か、と聞かれている。
とりあえず手のつくところから進めて行くと、2θが45度ぐらい(4θが90度ぐらい)ということまではたどりつく。しかし、そこから先への一歩が難しい。
解答は一般に予備校などで公開されている「45度との誤差が1度以下である」ことを示す方法を紹介するが、ここで思いついてもらいたいのは、π > 3.05 を示した“あの”問題の方法である。これは別解で示す。
いろいろな解法が考えられる良い難問。
解答
この三角形は、
52 + 122 = 132
を満たすから、長さが 5 , 12 である2辺にはさまれる角が直角であるような直角三角形である。いま、
![]()
であり、
![]()
であることから、![]() である。よって、
である。よって、
![]()
とすると、
![]()
がなりたつ。これに加法定理を用いて、
![]()
を tanα について解いて、
![]()
となる。![]() の範囲では、
の範囲では、
![]()
であるから、
![]()
であり、このαを度数法に直すと、
![]()
となりαは度数法で1度未満である。よって、
![]()
すなわち、
![]()
だから、 n = 22 である。
解説
別解
解答で紹介した方法は、たまたま2θが45度に近い角度であったことがポイントである。しかし、nθがよく知られている三角比の値に近い角度にならない場合には、この方法は使えない。
そこで、次の別解である。これを思いつく理由は、

の問題で行う上手な評価である。上の問題も必ずチェックしてもらいたい。
【別解】
与えられた三角形を図のように△ABCとおき、求める角度を弧度法表示の x [ rad ] とする。
図のように、長さ 12 の辺を 1 伸ばして、中心角θ、半径 13 の扇形ACDを考えると、このとき弧CDの長さは定義から 13x である。
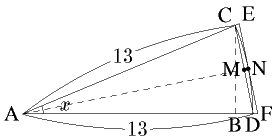
さらに、図のように線分CDの中点を M とし、直線AMと弧CDの交点を N とし、Nを通り線分CDにに平行な線分EFを引くと、△ACD ∽ △AFEとなる。この相似比を考えよう。
![]()
であるから、
![]()
である。△AMDは直角三角形だから、
![Rendered by QuickLaTeX.com \[ \text{AM} = \sqrt{13^2 - \left( \frac{\sqrt{26}}{2} \right)^2} = \cdots = \frac{5}{2}\sqrt{26} \]](http://izu-mix.com/math/wp-content/ql-cache/quicklatex.com-a6e87c601fd0df534b2e0c119e5cc7bf_l3.png)
である。
AN = 13
であるから、△ACD と △AFE の相似比は
![]()
である。
さて、扇型ACDの面積 S は、
![]()
であり、これは△ADCより大きく、△AEFより小さい。
![]()
であり、
![Rendered by QuickLaTeX.com \[ \triangle \text{AEF} = \frac{65}{2} \times \left( \frac{\sqrt{26}}{5} \right)^2 = \frac{13 \cdot 5}{2} \times \frac{13 \times 2}{5^2} = \frac{13^2}{5} \]](http://izu-mix.com/math/wp-content/ql-cache/quicklatex.com-39fda619e4b390d9346f23e1123f246f_l3.png)
であるから、
![]()
すなわち、
(a) ![]()
である。
この x を度数法の θ° に直して考える。(a)式は、
![]()
ということであり、
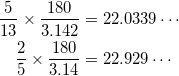
であるから、
![]()
であることが求められる。よって、 n = 22 である。

コメント