等確率でないサイコロ［1979 京都大・文理］

問題

　2人の人が1つのサイコロを1回ずつふり、大きい目を出したほうを勝ちとすることにした。ただし、このサイコロは必ずしも正しいものではなく、 k の目の出る確率は p_k である（ k = 1 , 2 , 3 , 4 , 5 , 6 ）。このとき
(1)　引き分けになる確率 P を求めよ。
(2)　 $P \geqq \dfrac{1}{6}$ であることを示せ。また、 $P=\dfrac{1}{6}$ ならば、 $p_k=\dfrac{1}{6}$ である（ k = 1 , 2 , 3 , 4 , 5 , 6 ）ことを示せ。

イズミの解答への道

解答

(1)　2人とも i の目を出す確率は、 $p_i^2$ であるから、

$\bm{P = p_1^2 + p_2^2 + p_3^2 + p_4^2 + p_5^2 + p_6^2}$

である。

(2)　コーシー・シュワルツの不等式より、

$( p_1 + p_2 + p_3 + p_4 + p_5 + p_6)^2 \leqq (1^2 + 1^2 + 1^2 +1^2 + 1^2 + 1^2 )(p_1^2 + p_2^2 + p_3^2 + p_4^2 + p_5^2 + p_6^2 )$

すなわち、

$1 \leqq 6P$

すなわち、

$P \geqq \frac{1}{6}$

であり、等号成立は p₁ = p₁ =p₂ = p₃ = p₄ = p₅ = p₆ となり、題意は示された。

解説

コーシー・シュワルツの不等式

　この問題は、(2)がポイント。形を見てすぐコーシー・シュワルツを思いつけるか、ということを問われている問題と言っても過言ではありません。
　コーシー・シュワルツの不等式というのは、、

$(ax + by )^2 \geqq (a^2 +b^2)(x^2 + y^2)$

が成り立つ（統合性率は a : b = x : y のとき）というもので、これは文字数が増えても同様に、

$(x_1 y_1 + x_2 y_2 + \cdots + x_n y_n )^2 \leqq (x_1^2 + x_2^2 + \cdots + x_n^2)(y_1^2 + y_2^2 + \cdots + y_n^2)$

が成り立つというものです。今回は n = 6 の場合の式を利用しています。
　ところで、こんな複雑な式は覚えるにはなかなか苦労します。実はこの不等式は、ベクトルの内積と関連付けて覚えると、とても覚えやすくなります。
　ベクトルの内積の公式は、

$\overrightarrow{p} \cdot \overrightarrow{q} = |\overrightarrow{p} ||\overrightarrow{q}| \cos \theta$

でした（cosθは $\overrightarrow{p},\overrightarrow{q}$ の為す角）。
　ここで、 $\overrightarrow{p} = ( a , b ) , \overrightarrow{q} = ( x , y )$ とすれば、この公式は、

$ax + by = \sqrt{a^2+b^2} \sqrt{x^2+y^2} \cos \theta$

となり、これを辺々2乗すると、

$(ax + by)^2 = (a^2 +b^2)(x^2 + y^2) \cos^2 \theta$

となります。 $\cos \theta$ は $\theta$ がどのような値であっても $-1 \leqq \cos \theta \leqq 1$ なので、

$(ax + by)^2 \leqq (a^2 +b^2)(x^2 + y^2)$

だといえます（等号成立は $cos \theta = 1$ のとき）。

　ところで、この内積の関係式は空間ベクトルでも同様でした。つまり3次元のベクトル

$\overrightarrow{p} = ( x_1 , x_2 , x_3 ) , \overrightarrow{q} = ( y_1 , y_2, y_3 )$

から、

$(x_1 y_1 + x_2 y_2 +x_3 y_3 )^2 \leqq (x_1^2 + x_2^2 + x_3^2)(y_1^2 + y_2^2 + y_3^2)$

が成り立つということです。
　ここで、これを n 文字に拡張しましょう。つまり、

$\overrightarrow{p} = ( x_1 , x_2 , \cdots , x_n ) , \overrightarrow{q} = ( y_1 , y_2, \cdots , y_n )$

だと考えて、それでも内積の定義が成り立つとするのです。すると、同様の議論から、コーシー・シュワルツの公式が導くことができます。

　n次元のベクトルなんて考えたことはない、とおっしゃるかもしれませんが、まずはこの不等式を覚えるための方法だと思ってください。
　大学では、線形代数学という分野でn次元のベクトルを学びます。このときにn次元のベクトルの内積についても、高校で学んだ内積の定義

$\overrightarrow{p} \cdot \overrightarrow{q} = |\overrightarrow{p} ||\overrightarrow{q}| \cos \theta$

を満たすように内積を定義します。つまり、理論的にも間違ったことではなく、正式にコーシー・シュワルツの不等式と内積はつながった概念だということができるのです。

　冒頭の話に戻りますが、この問題では、問題の式の形を見たときに、コーシー・シュワルツを思い出せるかがポイントです。 ax + by + czのような形や、ax² + by² + cz²のような形を見たときには、このコーシー・シュワルツの不等式をちらっと思いだせるようにしておくとよいでしょう。

別解

　(2)は以下のように解くこともできますが、数式だけで思いつくのはちょっと難しいですが、等号成立条件にあるように、Pが最小値になるのは全ての面の出る確率が等しいときだという発想を持つと、ここに気付けるかもしれません。

　実数の二乗和は正数になるので、

$\begin{align*} &\left(p_1 - \frac{1}{6} \right)^2+ \left(p_2 - \frac{1}{6} \right)^2+ \left(p_3 - \frac{1}{6} \right)^2 \\ &\qquad + \left(p_4 - \frac{1}{6} \right)^2+ \left(p_5 - \frac{1}{6} \right)^2+ \left(p_6 - \frac{1}{6} \right) \\ &= P - \frac{1}{3}(p_1 + p_2 + p_3 + p_4 + p_5 + p_6) + \frac{6}{36} \\ &= P - \frac{1}{3} + \frac{1}{6} \geqq 0 \end{align*}$

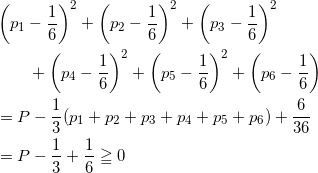
であるから、

$P \geqq \frac{1}{6}$

であることが示される。また等号成立は、 $p_1 = p_2 = p_3 = p_4=p_5= p_6 =\dfrac{1}{6}$ のときである。