1と2だけでできる数列［2015 慶應大・薬*］

問題

　{ a_n }は、数字の 1 と 2 だけで作ることのできる自然数を小さい順に並べた数列である。
　　{ a_n } : 1, 2, 11, 12, 21, 22, 111, ……
このとき、
(1) a₁₀ , a₁₅ を求めよ。
(2) $\displaystyle \sum_{k=7}^{14} a_k$ を求めよ。
(3)　{ a_n } のうち、 m 桁である項の総和を求めよ。

※もともとは穴埋め問題である。

イズミの解答への道

解答

(1)　書き出して考える。途中までは問題文にある。
　　a₇ = 111, a₈ = 112, a₉ = 121, a₁₀ = 122,
　　a₁₁ = 211, a₁₂ = 212, a₁₃ = 221, a₁₄ = 222,
　　a₁₅ = 1111
となる。

(2)　(1)で書きだした結果より、求める和は、
　　111 + 112 + 121 + 122 + 211 + 212 + 221 + 222
ここで、1項目と8項目の和、2項目と7項目の和、3項目と6項目の和、4項目と5項目の和はすべて 333 になることから、
　= ( 111 + 222 ) + ( 112 + 221 ) + ( 121 + 212 ) + ( 122 + 211 )
　　= 333 × 4 = 1332
となる。

(3)　1と2でできるm桁の自然数は、各桁が1か2であることから 2^m個ある。また、(2)で考えたように、1と2でできるm桁の自然数は、 11…1(m桁) から始まり 22…2(m桁) で終わるが、これの k 個目と 2^m-k 個目の合計は、 33…3(m桁) となる。
　以上のことから、m桁である項の総和は、

$\begin{align*} &\underbrace{33\cdots3}_{m} \times \frac{2^m}{2} \\ &=3 \times \frac{10^m- 1}{10 -1} \times 2^{m-1} \\ &=\bm{\frac{2^{m-1}(10^m -1)}{3}} \end{align*}$

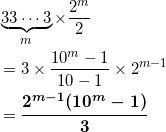
である。

解説

2進法

　この問題ように、ある特別な数字だけを使用して数を数えていく問題はよく出題されるが、 n 進法という考え方を用いると非常に明確になる。n進法とは正確には、 0, 1 , … , n-1 の n 個の数字を用いて数をあらわすもので、例えば本来の2進法は、
　　0 , 1 , 10 , 11 , 100 , 101 , 110 , 111 , …
のように数を数えていくものである。これはいわゆる普通の数字である10進法の、
　　0 , 1 , 2 , 3 , 4 , 5 , 6 , 7 , …
と対応しており、たとえば10進数の 5 が 2進数の 101 に対応していることは
　　5₍₁₀₎ = 101₍₂₎
のように表す。