関数方程式（tanh x）［2007 京都大・理乙］

問題

　すべての実数で定義され何回でも微分できる関数 f ( x ) が f ( 0 ) = 0 , f ‘ ( 0 ) = 1 を満たし、さらに任意の実数 a , b に対して 1 + f ( a ) f ( b ) ≠ 0 であって、

$f ( a+ b) = \frac{f(a)+f(b)}{1+f(a)f(b)}$

を満たしている。
(1)　任意の実数 a に対して、 $- 1 < f ( a ) < 1$ であることを証明せよ。
(2)　y = f ( x ) のグラフは x > 0 で上に凸であることを証明せよ。

イズミの解答への道

　(1)から難しい。類題経験がモノをいうタイプの問題です。連続関数の値域が制限されるということと、f ( 0 ) で値が定義されていることを考えれば、 f ( x ) = 1 , – 1 となり得ない（このような式を満たす x が存在しない）ことを示せば、 – 1 < f ( a ) < 1 であることが証明できます。

解答

(1)　f ( x ) = 1 あるいは f ( x ) = -1 を満たす x が存在しないことを背理法によって証明する。
　f ( a ) = 1 を満たす a が存在するとすると、

$f(0) = f( a-a) = \frac{f(a)+f(-a)}{1+f(a)f(-a)} = \frac{1+f(-a)}{1+f(-a)} = 1$

となり、 f ( 0 ) = 0 に矛盾するため、 f ( a ) = 1 となる a は存在しない。同様に f ( a ) = -1 を満たす a を仮定しても矛盾するため、 f ( a ) = -1 を満たす a は存在しない。
　よって、 f ( x ) = 1 あるいは f ( x ) = -1 を満たす x は存在しない。いま、 f ( 0 ) = 0 であることと、 f ( x) が（微分可能であることから）連続関数であることから、任意の実数 a に対して、 – 1 < f ( a ) < 1 である。 (2)

$\begin{align*} f'(x) &= \lim_{h \to 0} \frac{f(x+h)-f(x)}{h} \\ &=\lim_{h \to 0} \frac{1}{h} \left( \frac{f(x)+f(h)}{1+f(x)f(h)} - f(x) \right) \\ &=\lim_{h \to 0} \frac{1}{h} \cdot \frac{f(x) + f(h) - f(x) - \{ f(x) \}^2 f(h)}{1+f(x)f(h)} \\ &=\lim_{h \to 0} \frac{f(h)}{h} \cdot \frac{1- \{ f(x) \}^2 }{1+f(x)f(h)} \\ &=f'(0) ( 1 - \{ f(x) \}^2 ) \\ &=1 - \{ f(x) \}^2 \end{align*}$

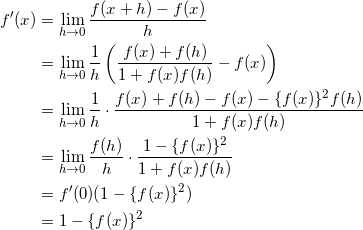
である。ここで(1)の結果より、
　　　1 – { f ( x ) }² > 0
であるから、
　　　f ‘ ( x ) > 0
である。よって、 f ( 0 ) = 0 と f ‘ ( x ) > 0 であることから、 x > 0 において
　　　f ( x ) > 0
である。
　　f ‘ ( x ) = 1 – { f ( x ) }²
をさらに x で微分して、
　　f ” ( x ) = – 2f ( x ) f’ ( x )
となるから、 x > 0 において、
　　f ’’ ( x ) < 0 であることから、与えられた関数 f ( x ) は x > 0 において上に凸であることが示された。

解説

奇関数であることを示す

　有名な関数方程式であるので、同じ関数についてさまざまな問題が出題されている。「すべての x で微分可能であること」は、
　　f ‘ ( x ) = 1 – { f ( x ) }²
ということから示され、「 f ( x ) は増加関数であること」は、
　　　1 – { f ( x ) }² > 0
ということから示される。（(1)で示したとおり、すべての x について – 1 < f ( x ) < 1 。）　　最後ににもう1つ、よく出題されるポイントとして、「この関数が奇関数であること」を示しておこう。これは、a = x = -b を代入すると、

$f(0) = \frac{f(x) + f(-x)}{1 + f(x)f(-x)} = 0$

より、
　　f ( x ) = f ( -x )
となるので、 f ( x ) は奇関数であることが示された。

題意を満たす f ( x ) を求める

　(2)で示した微分方程式
　　f ‘ ( x ) = 1 – { f ( x ) }²
を解くことで、題意を満たす f ( x ) を求めることができる。 y = f ( x ) とおいて、変数分離形として変数を分離すると、

$\begin{align*} y' &= 1 - y^2 \\ \frac{dy}{dx} &= 1 - y^2 \\ \frac{1}{1-y^2} dy &= dx \\ \end{align*}$

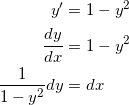
となるので、両辺を積分して、

$\begin{align*} \int \frac{1}{(1+y)(1-y)}dy &= \int dx \\ \frac{1}{2} \int \left( \frac{1}{1+y} + \frac{1}{1-y} \right) dy &= \int dx \\ \frac{1}{2} \left( \log (1+y) - \log ( 1 -y) \right) &= x + C' \\ \log \frac{1+y}{1-y} &= 2x + c'' \\ \frac{1+y}{1-y} &= Ce^{2x} \end{align*}$

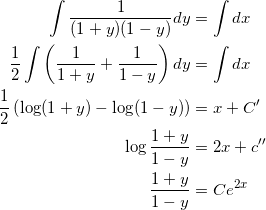
となる。これを y について解くと、

$\begin{align*} 1 + y &= (1 -y)Ce^{2x} \\ y + Ce^{2x}y &= Ce^{2x} -1 \\ y &= \frac{Ce^{2x}-1}{Ce^{2x}+1} \\ \end{align*}$

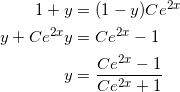
となる。 f ( 0 ) = 0 であることから、 C = 1 となるので、

$y = f(x) = \frac{e^{2x}-1}{e^{2x}+1} = \frac{e^x - e^{-x}}{e^x + e^{-x}}$

となる。
　
　これは双曲線関数と呼ばれるもののうちの tanh x （ハイパボリックタンジェント）という関数である。双曲線関数には三角関数と同じような性質があり、今回の関数方程式は tanh x の加法定理であり、三角関数の tan x の加法定理と似ていることも分かる。