問題
a > 0 とする。 y = e-x2 と x 軸、 y 軸、および直線 x = a で囲まれた図形を、 y 軸の周りに1回転してできる回転体を A とする。
(1) Aの体積を求めよ。
(2) 点 ( t , 0 ) ( -a ≦ t ≦ a ) を通りx軸と垂直な平面によるAの切り口の面積を S ( t ) とするとき、不等式
![]()
を示せ。
(3) 不等式
![]()
を示せ。
イズミの解答への道
解答
(1)
![]()
ここで、![]() より、
より、![]() より、
より、
![Rendered by QuickLaTeX.com \begin{align*} V &= \pi a^2 e^{-a^2} - \pi \int_{-e^{a^2}}^1 \log y dy \\ &=\pi a^2 e^{-a^2} - \pi [ y \log y - y ]_{-e^{a^2}}^1 \\ &=\bm{ \pi ( 1 - e^{-a^2} )} \end{align*}](http://izu-mix.com/math/wp-content/ql-cache/quicklatex.com-ea0f021f9ca6a3a2f29f866c26121aed_l3.png)
である。
(2) 立体Aを式で表すことを考える。
まず、![]() を y 軸を軸に回転させたときにできる曲面をPとする。また、ここで
を y 軸を軸に回転させたときにできる曲面をPとする。また、ここで ![]() は偶関数である。
は偶関数である。
P上の点を ( x , y , z ) とおいたとき、
-
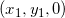 については、
については、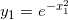 が成り立つ。
が成り立つ。
- 次に、
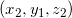 について、
について、 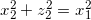 が成り立つから、
が成り立つから、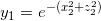 が成り立つ。このことから、曲面Pの表面上の点は、
が成り立つ。このことから、曲面Pの表面上の点は、
![Rendered by QuickLaTeX.com \[ y = e^{-(x^2 + z^2)} \]](http://izu-mix.com/math/wp-content/ql-cache/quicklatex.com-0c51b438b6d59c83f19475c302780ceb_l3.png)
である。
実際の立体Aはこの(原点を含む側の)内部の点の集合と、円柱![]() の共有部分だから、
の共有部分だから、
![Rendered by QuickLaTeX.com \[ \begin{cases} 0 \leqq y \leqq e^{-(x^2 +z^2)} \\ x^2 + y^2 \leqq a^2 \end{cases} \]](http://izu-mix.com/math/wp-content/ql-cache/quicklatex.com-fb24fa78326ae4be93896cc9088911f6_l3.png)
となる。
さて、Aを平面 x = t で切断した時の切り口は、
![Rendered by QuickLaTeX.com \[ \begin{cases} -\sqrt{a^2-t^2} \leqq z \leqq \sqrt{a^2-t^2} \\ 0 \leqq y \leqq e^{-(z^2+t^2)} \end{cases} \]](http://izu-mix.com/math/wp-content/ql-cache/quicklatex.com-33a994eea0b425ae2041dfbf56ccd9f0_l3.png)
より、この面積は、
![]()
となる。ここで、![]() であるから、
であるから、
![]()
となり、題意は示された。
(3) いま、![]() とおくと、(2)より、
とおくと、(2)より、
![]()
であり、さらに![]() より、
より、
![]()
であり、(1)より、
![]()
であることを利用して、
![]()
が示された。
解説
回転体
この問題のテーマはこのあと取り上げる「ガウス積分」であるが、その前にこの問題を解くなかで思い出した問題があるので、そちらを紹介しておきたい。1983年東大の回転放物面に関する問題である。
どちらの問題でも共通する知識として、次の補題は覚えていて損はない。
z = f ( x ) (ただし f ( x ) は偶関数)を z 軸で回転した図形は、
![]()
である。
東大の問題は、次のページで扱う。
ガウス積分と重積分
本文で扱われた関数を、定義域 ( -∞ , ∞ ) で積分したもの、すなわち、
![]()
をガウス積分といい、この値は ![]() になることが知られている。この積分は高校では正規分布の学習において、証明なしに利用して良いということになっている。なぜ証明なしに利用して良いのかというと、これは大学で学ぶ重積分の計算を用いないと求められないからである。
になることが知られている。この積分は高校では正規分布の学習において、証明なしに利用して良いということになっている。なぜ証明なしに利用して良いのかというと、これは大学で学ぶ重積分の計算を用いないと求められないからである。

コメント