対数関数の定義［2009 順天堂大・医］

問題

　次の問に答えよ。答えだけではなく式・説明など解答の途中の経過を示すこと。
(1)　関数 y = f ( x ) の値域の定義を述べよ。
(2)　関数 y = f ( x ) があるとき、逆関数が存在する条件と逆関数の定義を述べよ。
(3)　対数関数を指数関数により定義せよ。
(4)　対数関数の底の変換公式を書きなさい。さらに、指数法則より底の変換公式を示しなさい。

［2009 順天堂大・医］

イズミの解答への道

　00年代に順天堂大で毎年のように出題されていた「定理・公式の証明」です。近年ではこのようなタイプの問題も多いので、定義を述べたり、公式を証明したりする練習をしていない人は、必ずやっておきましょう。

解答

(1)　変数 x が定義域内の値をうごくとき、その値 x = a に応じて定まる変数 y の値 f ( a ) の取り得る値の範囲をいう。

(2)　「値域の任意の値 b に対して、 b = f ( a ) となる定義域の値 a がただ1つ存在すること」ことが存在条件である。
　逆関数とは、f の値域を定義域とし、値域に対応するただ1つの定義域の値 a を対応させる関数をいう。

(3)　指数関数とは、y = a^x （ x は実数全体、 a > 0 , a ≠ 1 ）を満たす関数である。0 < a < 1 のとき単調減少、 a > 1 のとき単調増加の関数であるから、 x_i ≠ x_j であれば f ( x_i ) ≠ f ( x_j ) である。すなわち値域に対応する定義域の値はただ1つであるから、指数関数には逆関数が存在する。これを対数関数と定義して、 y = log_ax と表す。

(4)　底の変換公式とは、 a > 0 , a ≠ 1 , b > 0 , c > 0 , c ≠ 1 に対して、

$\log_a b = \frac{\log_c b}{\log_c a}$

というものである。
　log_ab = x , log_cb = y , log_ca = z とおくと、対数関数は指数関数の逆関数であるから、 a^x = b , c^y = b , c^z = a が成り立つので、
　　b = a^x = c^y
であり、 a = c^z だから、
　　b = ( c^z )^x = c^y
が成り立つ。指数法則より、
　　b = c^zx = c^y
となるから、対数関数の定義より、
　　z^x = log_cb = y
であり、 z^x = y において、 z ≠ 0 であるから両辺を z で割って、

$x = \frac{y}{z}$

となる。ここで、 log_ab = x , log_cb = y , log_ca = z であるから、底の変換が示された。

解説

記述の仕方

　近年頻繁に見かけるようになった公式や定義を証明する問題であるが、このような問題における記述の注意点を1つだけ挙げておく。それは、証明すべき公式以外の公式を使うときには「○○の公式より、」だとか「定義により、」といった説明を加えることである。
　普通の問題を解く場合には、知っている公式や定義は当たり前のように解けばよいが、このように定義や公式を導くときには、その過程を誰にでも分かるように、どの公式を使ったのか、どの定義を使って導いたのか、そのような細かい部分をきちんと書くようにしたい。
　当然だが、今から証明する公式を途中で用いることのないように気をつけよう。循環論法になってしまう。

類題1

　順天堂大の過去問から、指数・対数関数が関係する問題を紹介する。まずは本文と同様、指数対数の基本的な公式を定義から求める問題である。

　次の問に答えよ。答えだけではなく式・説明など解答の途中の経過を示すこと。なお、本問中に現れる文字はすべて実数であり、(2)、(3)、(4)において、 a は(1)で答えた条件を満たすものとする。
(1)　関係式 L = a^l において、対数関数を用いて l を a , L で表せ。なお、そう表せるための a , L の条件を記せ。
(2)　L = a^l , M = a^m , N = aⁿ の間に L = MN の関係があるとき、 l , m , n の関係式を求めよ。
(3)　正の実数 M , N に対して、

$\log_a \frac{M}{N} = \log_a M - \log_a N$

を示せ。
(4)　( a^m )^k = a^mk を用いて、
　　log_aM^k = k log_aM
となることを示せ。

［2003 順天堂大・医］

【解答】
(1)　l = log_aL

(2)　指数法則より、
　　　a^l = a^m・aⁿ = a^m+n
であるから、
　　l = m + n
となる。

(3)　指数法則より、

$\frac{M}{N} = \frac{a^m}{a^n} = a^{m-n}$

であるから、両辺に a を底とした対数をとれば、その定義より、

$\log_a \frac{M}{N} = m - n$

であり、 m = log_aM , n = log_aN であるから、

$\log_a \frac{M}{N} = \log_a M - \log_a N$

が示された。

(4)　( a^m )^k = a^mk より
　　M^k = a^mk
が成り立つ。ここに a を底とした対数を取れば、
　　log_aM^k = m^k = k log_aM
となり示された。

類題2

　続いても順天堂大の過去問である。数学IIIの知識が必要になる問題です。

　次の問に答えよ。答えだけではなく式・説明など解答の途中の経過をも示すこと。
(1)　関数 y = f ( x ) について、その逆関数が存在するのは、f ( x ) がどのような関数の場合か述べよ。
(2)　微分可能な関数 y = f ( x ) に対して、その逆関数 f^-1 ( x ) が存在すると仮定する。また、ある値 a に対して、 f’ ( a ) ≠ 0 であり、 b = f ( a ) とする。このとき、 x = b における f-1 ( x ) の微分係数を f を使って表せ。
(3)　 $\displaystyle \lim_{t \to 0} \frac{e^t -1}{t} =1$ と微分の定義より、指数関数 y = a^x の導関数を求めよ。ただし、a > 0 かつ a ≠ 1 とする。
(4)　(3)の結果を使って、対数関数 y = log_ax の導関数を求めよ。

［2004 順天堂大・医］

【解答】
(1)　今回の問題の(2)と同じです。 y = f ( x ) の値域の任意の値 b に対して、 b = f ( a ) となる定義域の値 a がただ1つ存在するとき。

(2)　y = f^-1 ( x ) の微分係数を求めるので、y = f^-1 ( x ) とおくと x = f ( y ) が成り立つ。ここで f^-1 ( x ) = g ( x ) とおくと、
　　　y = g ( f ( y ) )
が成り立つので、この両辺を y で微分すると、合成関数の微分法の公式より、
　　　1 = g ‘ ( f ( y ) ) ・ f ‘ ( y )
　　　　= g ‘ ( x ) ・ f ‘ ( y )
より、 f ‘ ( y ) ≠ 0 の範囲で

$g'(x) = \frac{1}{f'(y)}$

が成り立つ。いま、 b = f ( a ) だとすると
　　　a = f^-1 ( b ) = g ( b )
であるから、 f ‘ ( a ) ≠ 0 のとき、
　　
が成り立つ。

(3)

$\frac{a^{x+h} -a^x}{h} = a^x \cdot \frac{a^h - 1}{h}$

であり、ここで
　　a = e^{log a} より a^h = e^{h log a}
であることを利用すると、

$\frac{a^{x+h} -a^x}{h} = a^x \cdot \frac{a^{h \log a} - 1}{h \log a} \cdot \log a$

と変形できる。よって、

$\begin{align*} (a^x)' &= \lim_{h \to 0} \frac{a^{x+h} - a^x}{h} \\ &=\lim_{h \to 0} \left( a^x \cdot \frac{a^{h \log a} - 1}{h \log a} \cdot \log a \right) \\ &=a^x \cdot 1 \cdot \log a \\ &=\bm{ a^x \log a } \end{align*}$

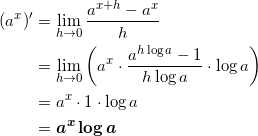
となる。

(4)　y = a^x は単調な連続関数だから逆関数が存在する。逆関数は、 y = log_ax である。よって、(2)の結果を用いると、

$( \log_a x)' = \frac{1}{(a^y)'} = \frac{1}{a^y \log a} = \bm{\frac{1}{x \log a}}$

である。（最後は逆関数の性質。具体的には a^y に y = log_ax を代入すれば a^y = x を得る。）

類題3

　最後は一風変わった問題です。教科書で学ぶ対数関数は指数関数の逆関数として学びますが、この問題では log x を特殊な形で定義します。数学はいろいろな定義を元に構築することができるということですね。
　この問題も数学IIIの知識が必要になります。

(1)
(i)　a > 0 , a ≠ 1 , M > 0 である実数 a , M に対し、 a を底とする M の対数 log_aM の定義を述べよ。
(ii)　a > 0 , b > 0 , c > 0 , a ≠ 1 , c ≠ 1 である実数 a , b , c に対し、底の変換公式

$\log_a b = \frac{\log_c b}{\log_c a}$

が成り立つことを示せ。
(2)　正の実数 x の自然対数 log x は

$\log x = \int_1^x \log \frac{1}{t} dt$

と表される。これを用いて、正の実数 x , y に対し、
　　log (xy) = log x + log y
が成り立つことを示せ。

［2015 上智大・理工］

【解答】
(1)　a^x = M を満たす x を log_aM と定義する。

(2)　log_ab = x , log_cb = y , log_ca = z とおくと、(1)の定義より
　　a^x = b , c^y = b , c^z = a
となる。前半の2式より、
　　a^x = c^y
であり、最後の式を代入して
　　( c^z )^x = c^y
となる。ここで指数の肩を比較して、
　　xz = y
が成り立つ。いま、 z ≠ 0 であるから、z で辺辺割って

$x = \frac{y}{z}$

すなわち、

$\log_a b = \frac{\log_c b}{\log_c a}$

が成り立つ。

(3)　与えられた式より、

$\begin{align*} \log (xy) &= \int_1^{xy} \frac{1}{t} dt \\ &=\int_1^x \frac{1}{t} dt + \int_x^{xy} \frac{1}{t} dt \end{align*}$

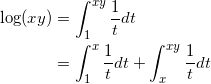
となり、ここで t = xu とおくと、dt = xdu であり、

$\begin{array}{c|ccc} t & x & \to & xy \\ \hline u & 1 & \to & y \end{array}$

となることから、

$\begin{align*} \log (xy) &= \int_1^x \frac{1}{t} dt + \int_1^y \frac{1}{u} du \\ &=\log x + \log y \end{align*}$

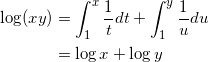
となり題意は示された。