問題
ある街から16世帯を無作為に選んで所得を調べたところ、度数分布表は以下のようになった。

(1) 所得の平均値、中央値、標準偏差および範囲を求めよ。
(2) 上の表で所得1000万円の世帯の所得が、実は1000万円でなく9000万円であったとする。このとき、平均値、中央値、標準偏差および範囲を求めよ。
(3) (1)、(2)をもとに、平均値と中央値のどちらがどのような場合に資料の代表値として適切であるかを150字以内で述べよ。
イズミの解答への道
平均値と中央値の特徴をきちんと理解していますか?という問題で、とても有名な問題です。この問題を通じてキチンと抑えておきましょう。(1)と(2)は公式通りです。
解答
(1) 平均値は、
![]()
より、700万円。
中央値は、所得の低い方から7世帯目、8世帯目の平均値で、どちらも700万円だから、700万円。
標準偏差 s は、
![]()
より、
![]()
だから、![]() 万円である。
万円である。
範囲は、1000 – 400 = 600万円。
(2) 同様に、平均値は、
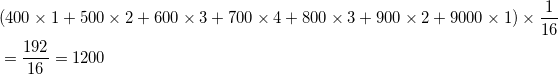
より、1200万円。
中央値は、変わらず700万円。
標準偏差 s’ は、
![]()
より、
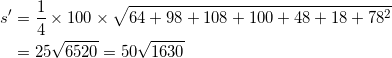
より、![]() 万円である。
万円である。
範囲は 9000 – 400 = 8600万円である。
(3) 平均値から大きく離れた値が少数含まれる場合は、平均値は母集団の傾向を示さない。実際(2)では平均値は1200万円だが、16世帯中15世帯は平均値より収入が低い。このような場合は中央値を用いるのが適切である。

コメント