四面体OABCが次の条件を満たすならば、それは正四面体であることを示せ。
条件:頂点A, B, C からそれぞれの対面を含む平面へ下ろした垂線は対面の外心を通る
ただし、四面体のある頂点の対面とは、その頂点を除く他の3つの頂点がなす三角形のことをいう。
イズミの解答への道
京大の頻出問題である、図形に関する証明問題です。この問題は素直で易しいので取り組んでもらいたい。
実は文系では条件が「対面の重心を通る」となった問題が出題されており、こちらはもう少し骨が折れる。
解答
頂点Aから下ろした垂線と対面OBCが交わる点をHとする。Hは外心だから、
HO = HB = HC
また、AH⊥平面OBCだから、
∠AHO = ∠AHB = ∠AHC = 90°
である。よって、AHが共通であることを加味すると、
△AHO ≡ △AHB ≡ △AHC
がいえる。よって、OA = AB = AC である。
同様に B , C から垂線を下ろした場合にも、
BO = BA = BC
CO = CA = CB
がいえるので、これらより、
AB = AC = AO = BC = BO = CO
となり、すべての面が正三角形である。よって四面体OABCは正四面体である。
解説
類題
同じく2016年の京都大の文系の問題を見てみよう。
四面体OABCが次の条件を満たすならば、それは正四面体であることを示せ。
条件:頂点A, B, C からそれぞれの対面を含む平面へ下ろした垂線は対面の重心を通る
ただし、四面体のある頂点の対面とは、その頂点を除く他の3つの頂点がなす三角形のことをいう。
【解答】
頂点Aから対面に下ろした垂線の足をGA、頂点Bから対面に下ろした垂線の足をGBとする。
GAとGBはそれぞれ対面の重心であるから、線分AGAと線分BGBは、四面体OABCの重心Gで交わる。つまり、線分AGAと線分BGBは一つの平面上にある。そしてその平面とは、OCの中点をMとしたときに、△ABMで表される(△ABMを含む平面)。
次に、AGAと面BCOは垂直だから、
AGA⊥CO
であり、BGBと面ACOは垂直だから、
AGB⊥CO
であるから、COと△ABMは垂直である。よって、
CO⊥BM
であり、MはCOの中点であることから、BMはCOの垂直二等分線であるといえる。よって、
BC = BO
である。
すべての2つの垂線から同様の議論をすることができ、これにより、すべての辺が等しいことが示される。よって、四面体OABCは正四面体であることが示される。
別解:ベクトルで
このような問題が出たとき、「こうすれば必ず解ける」という王道はないのだが、今回紹介した2問は、ベクトルで進めればなんとかなる。以下ではその計算を紹介しておこう。ゴリ押しではあるが、受験本番では一つの候補となるだろう。
【冒頭の問題の別解】
まず、![]() とおく。
とおく。
Aから下ろした垂線の足を HA とおくと、 HA は△OBCの外心となるので、
HAO = HAB = HAC
であるから、![]() とおくと、
とおくと、
![]()
となる。これより、
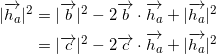
となるので、
(a) ![]()
(b) ![]()
となる。
また、AHAは垂線であるから、![]() ⊥平面OCB であることから、
⊥平面OCB であることから、
![]()
である。これより、
![]()
すなわち、
![]()
であるから、これを(a)式、(b)式に代入して、
(a’) ![]()
(b’) ![]()
となる。
同様に、Bから下ろした垂線、Cから下ろした垂線についても同様に計算すると、
(c) ![]()
(d) ![]()
(e) ![]()
(f) ![]()
が成り立つ。
これらより、![]() となり、
となり、
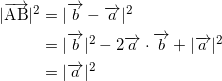
であり、同様に、![]() が示される。
が示される。
以上より、
OA = OB = OC = AB = BC = AC
であるから、四面体OABCは正四面体であることが示された。
【類題の別解】
まず、![]() とおく。
とおく。
Aから下ろした垂線の足を GA とおき、![]() とおく。 GA は△OBCの重心となるので、
とおく。 GA は△OBCの重心となるので、
(a) ![]()
となる。
また、AGAは垂線であるから、![]() ⊥平面OCB であることから、
⊥平面OCB であることから、
![]()
である。これより、
![]()
であり、(a)式を代入して整理すると、
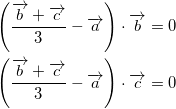
すなわち、
(b) ![]()
(c) ![]()
となる。
同様に、Bから下ろした垂線、Cから下ろした垂線についても同様に計算すると、
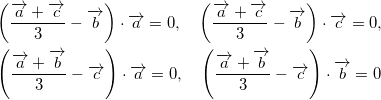
より、
(d) ![]()
(e) ![]()
(f) ![]()
(g) ![]()
が成り立つ。
これらより、![]() となり、
となり、
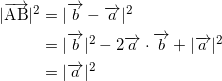
であり、同様に、![]() が示される。
が示される。
以上より、
OA = OB = OC = AB = BC = AC
であるから、四面体OABCは正四面体であることが示された。

コメント