問題
数列の和 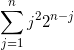 を求めよ。
を求めよ。
イズミの解答への道
「等差×等比の和」は超基本的な問題ですが、この問題は等差数列ではないので、試験で出題されると慌ててしまいそうです。それでも試しにその方法をやってみれば、実は2回繰り返すことで解ける、というところがポイントです。
別解で示した方法も覚えておくとよいでしょう。
解答
求める和を S とすると、
![Rendered by QuickLaTeX.com \[ \begin{array}{rrrrrrr} S =& 1^2 \cdot 2^{n-1} &+ 2^2 \cdot 2^{n-2} &+ 3^2 \cdot 2^{n-3} &+ \cdots +& n^2 \cdot 2^0 & \\ \displaystyle \frac{1}{2}S =& &+ 1^2 \cdot 2^{n-2} &+ 2^2 \cdot 2^{n-3} &+ \cdots +& (n-1)^2 \cdot 2^0 &+ n^2 \cdot 2^{-1} \\ \end{array} \]](http://izu-mix.com/math/wp-content/ql-cache/quicklatex.com-f1e1e1d5db823ce42510d2838664c6d6_l3.png)
であるから、上の式から下の式を引いて、
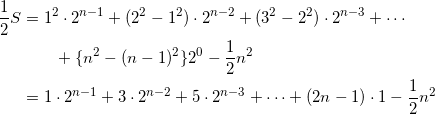
となる。
さらに同様に、
![Rendered by QuickLaTeX.com \[ \begin{array}{rrrrrll} \displaystyle \frac{1}{2}S =& 1 \cdot 2^{n-1} &+ 3 \cdot 2^{n-2} &+ \cdots +& (2n-1) \cdot 2^0 & \displaystyle -\frac{1}{2}n^2 & \\ \displaystyle \frac{1}{4}S =& &+ 1 \cdot 2^{n-2} &+ \cdots +& (2n-3)\cdot 2^0 &+ \displaystyle \frac{1}{2}(2n-1) & \displaystyle -\frac{1}{4}n^2 \\ \end{array} \]](http://izu-mix.com/math/wp-content/ql-cache/quicklatex.com-824b7d89883d3f9b7f221c9d96ccee57_l3.png)
の上の式から下の式を引いて、
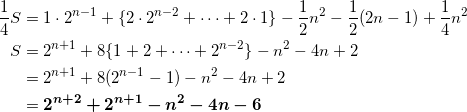
 大学入試数学演習
大学入試数学演習 数列の和 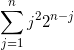 を求めよ。
を求めよ。
「等差×等比の和」は超基本的な問題ですが、この問題は等差数列ではないので、試験で出題されると慌ててしまいそうです。それでも試しにその方法をやってみれば、実は2回繰り返すことで解ける、というところがポイントです。
別解で示した方法も覚えておくとよいでしょう。
求める和を S とすると、
![Rendered by QuickLaTeX.com \[ \begin{array}{rrrrrrr} S =& 1^2 \cdot 2^{n-1} &+ 2^2 \cdot 2^{n-2} &+ 3^2 \cdot 2^{n-3} &+ \cdots +& n^2 \cdot 2^0 & \\ \displaystyle \frac{1}{2}S =& &+ 1^2 \cdot 2^{n-2} &+ 2^2 \cdot 2^{n-3} &+ \cdots +& (n-1)^2 \cdot 2^0 &+ n^2 \cdot 2^{-1} \\ \end{array} \]](http://izu-mix.com/math/wp-content/ql-cache/quicklatex.com-f1e1e1d5db823ce42510d2838664c6d6_l3.png)
であるから、上の式から下の式を引いて、
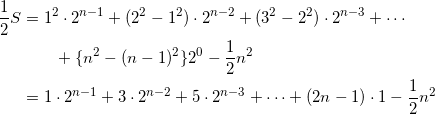
となる。
さらに同様に、
![Rendered by QuickLaTeX.com \[ \begin{array}{rrrrrll} \displaystyle \frac{1}{2}S =& 1 \cdot 2^{n-1} &+ 3 \cdot 2^{n-2} &+ \cdots +& (2n-1) \cdot 2^0 & \displaystyle -\frac{1}{2}n^2 & \\ \displaystyle \frac{1}{4}S =& &+ 1 \cdot 2^{n-2} &+ \cdots +& (2n-3)\cdot 2^0 &+ \displaystyle \frac{1}{2}(2n-1) & \displaystyle -\frac{1}{4}n^2 \\ \end{array} \]](http://izu-mix.com/math/wp-content/ql-cache/quicklatex.com-824b7d89883d3f9b7f221c9d96ccee57_l3.png)
の上の式から下の式を引いて、
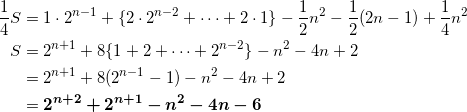
コメント