微分可能の定義に関する証明［2007 順天堂大・医］

　次の問に答えよ。答えだけではなく式・説明など解答の途中の経過を示すこと。
(1)　関数 f ( x ) が x = a で微分可能とはどういうことか、説明せよ。
(2)　「関数 y = f ( x ) が x = a で微分可能である」と「関数 y = f ( x ) が x = a で連続である」とはどのような関係にあるか述べよ。またそれを証明せよ。
(3)　ある区間 a < x < b で微分可能な関数 f ( x ) , g ( x ) について、導関数の定義から、関数の積 f ( x ) g ( x ) の導関数を求めよ。

［2007 順天堂大・医］

イズミの解答への道

　流行の「定理の証明」です。(1)や(3)はこれまでに他大学において出題されていますが、(2)は目新しい内容です。数学IIIの勉強は、どうしても計算が中心になってしまいがちですが、連続と微分可能性の関係は微積分の重要ポイントですから、是非覚えておきましょう。

解答

(1)　関数 f ( x ) が x = a で微分可能であるとは、極限値 $\displaystyle \lim_{x \to a} \frac{f(x) - f(a)}{x - a}$ が存在することである。

(2)　関数 y = f ( x ) について、『「 x = a で微分可能である」ならば「 x = a で連続である」（※）』は成立するが、逆（『「 x = a で連続である」ならば「 x = a で微分可能である」（※※）』）は成り立たない。

（※）の証明
　f ( x ) が x = a で微分可能であれば、

$\begin{align*} \lim_{x \to a} \{ f(x) - f(a) \} &= \lim_{x \to a} \left\{ \frac{f(x)-f(a)}{x-a} \times (x-a) \right\} \\ &= f'(a) \cdot 0 = 0 \end{align*}$

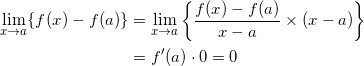
より、

$\lim_{x \to a} f(x) = f(a)$

となり、 x = a で連続であることが示される。

（※※）の証明
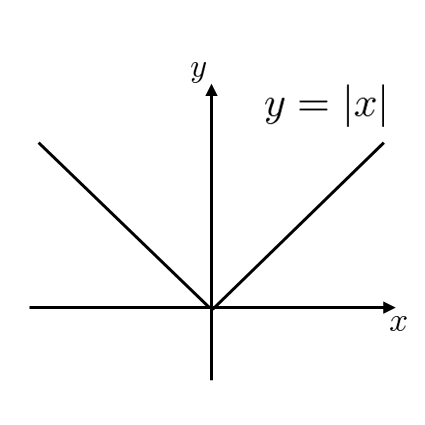
　反例として f ( x ) = | x | とすると、 x = 0 では連続だが微分可能ではない。実際、

$\begin{align*} &\lim_{x \to -0} \frac{f(x) - f(0)}{x- 0} = \lim_{x \to -0} \frac{-x-0}{x-0} = -1 \\ &\lim_{x \to 0} \frac{f(x) - f(0)}{x- 0} = \lim_{x \to 0} \frac{x-0}{x-0} = 1 \end{align*}$

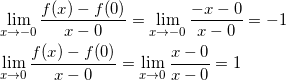
となることから、 f ( x ) は x = 0 で（連続だが）微分可能ではない。

(3)

$\begin{align*} &\{ f(x)g(x) \}' \\ &=\lim_{h \to 0} \frac{f(x+h)g(x+h) - f(x)g(x)}{h} \\ &=\lim_{h \to 0} \frac{f(x+h)g(x+h)-f(x)g(x+h)+f(x)g(x+h)-f(x)g(x)}{h} \\ &=\lim_{h \to 0} \left( \frac{f(x+h) -f(x)}{h} \cdot g(x+h) + f(x) \cdot \frac{g(x+h)-g(x)}{h} \right) \end{align*}$

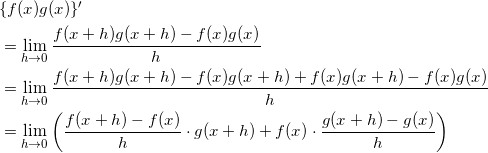
であり、ここで f ( x ) , g ( x ) は微分可能だったから、

$\lim_{h \to 0} \frac{f(x+h) - f(x)}{h} = f'(x) , \quad \lim_{h \to 0} \frac{g(x+h) - g(x)}{h} = g'(x)$

であり、 h → 0 のとき
　　g ( x + h ) → g ( x )
となるから、
　　{ f ( x ) g ( x ) }’ = f ‘ ( x ) g ( x ) + f ( x ) g ‘ ( x )
が成り立つ。

解説

類題1

　2002年の神戸大・理に同様の出題がある。それを紹介しておこう。

　関数 f ( x ) は任意の実数 x に対して定義されているとする。次の問に答えよ。
(1)　f ( x ) が x = a において微分可能であることの定義を述べよ。
(2)　次の2つの命題のうち正しい物を選び、それが正しい理由を示せ。
　(i)　f ( x ) が x = a において連続ならば、必ず、 f ( x ) は x = a において微分可能である。
　(ii)　f ( x ) が x = a において連続であっても、 f ( x ) は x = a において微分可能であるとは限らない。
(3)　関数 f ( x ) = cos x が x = a において微分可能であることを、(1)で答えた定義を用いて証明せよ。

［2002 神戸大・理］

解答

　(1)、(2)は上と同様である。特に、(2)は(ii)が正解であり、理由としては上の反例を上げれば良い。(3)のみ解答を紹介しておこう。
(3)　和積の公式

$\cos \alpha - \cos \beta = -2 \sin \frac{\alpha + \beta}{2} \sin \frac{\alpha - \beta}{2}$

を用いることで、

$\begin{align*} \lim_{h \to 0} \frac{\cos ( a + h) - \cos a}{h} &= \lim_{h \to 0} \frac{-2\sin \left( a + \frac{h}{2} \right) \sin \frac{h}{2}}{h} \\ &= - \lim_{h \to 0} \sin \left( a + \frac{h}{2} \right) \cdot \frac{\sin \frac{h}{2}}{\frac{h}{2}} \\ &= - \sin a \end{align*}$

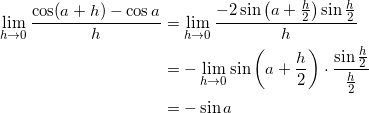
より、 f ( x ) = cos x は x = a において微分可能である。

類題2

　2015年の神戸大・理（後）でも再び微分可能性に関する出題がある。

　以下の問に答えよ。
(1)　関数 f ( x ) が x = a で微分可能であることの定義を述べよ。
(2)　関数 f ( x ) = | x² – 1 | e^-x は x = 1 で微分可能でないことを示せ。
(3)　関数 f ( x ) = | x² – 1 | e^-x の極値と、極値をとるときの x の値を求めよ。

［2015 神戸大・理（後）］

解答

　(1)は上の出題と全く同じである。