nまでの自然数の異なる2数の積の和［2007 筑波大］

問題

(1)　一般項 a_n が an³ + bn² + cn で表される数列 { a_n } において、
　　　n² = a_n+1 – a_n　( n = 1 , 2 , 3 … )
が成り立つように、定数 a , b , c を定めよ。
(2)　(1)の結果を用いて、
　　 $\displaystyle \sum_{k=1}^n k^2 = \frac{1}{6} n (n+1)(2n+1)$
となることを示せ。
(3)　1 , 2 , … , n の相違なる2数の積のすべての和を S ( n ) とする。たとえば、
　　　S ( 3 ) = 1×2 + 1×3 + 2×3 = 11
である。S ( n ) を n の 4 次式で表せ。

イズミの解答への道

　(3)が入試頻出の有名問題。受験までには1度は体験しておきましょう。(1)、(2)は和の公式を求める手順で、(3)で使用するので誘導がありますが、この結果は覚えてかなければなりません。(3)単体で出題されても回答できるようにしておきましょう。

解答

(1)　 a_n+1 – a_n
　　　= a ( n + 1 )³ + b ( n + 1 )² + c ( n + 1 ) – ( an³ + bn² + cn )
　　　= a ( 3n² + 3n + 1 ) + b ( 2n + 1 ) + c
　　　= 3an² + ( 3a + 2b ) n + a + b + c = n²
の恒等式が成り立つためには、
　　　3a = 1 , 3a + 2b = 0 , a + b + c = 0
であればよいから、これを解いて、
　　 $\displaystyle \bm{a = \frac{1}{3}, b= - \frac{1}{2} , c=\frac{1}{6}}$
である。

(2)

$\begin{align*} \sum_{k=1}^n k^2 &= (a_2 - a_1) + (a_3 -a_2) + \cdots + (a_{n+1} -a_n ) \\ &=a_{n+1} - a_1 \\ &=\frac{1}{3} (n+1)^3 - \frac{1}{2}(n+1)^2 + \frac{1}{6} (n+1) - \left( \frac{1}{3} - \frac{1}{2} + \frac{1}{6} \right) \\ &=\frac{1}{6} (n+1) \{ 2(n+1)^2 - 3(n+1) +1 \} \\ &=\frac{1}{6} (n+1) (2n^2 +n) \\ &=\bm{\frac{1}{6} n(n+1)(2n+1)} \end{align*}$

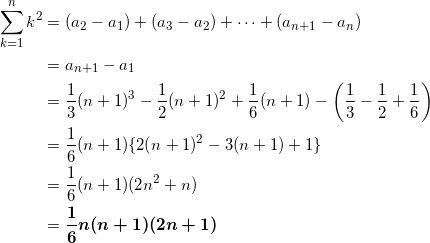
(3)　恒等式
　　( 1 + 2 + … + n )² = 1² + 2² + … + n² + 2 S ( n )
が成り立つから、これを S ( n ) について解いて、

$\begin{align*} S(n)&= \frac{1}{2} \left\{ (1+ 2+\cdots+n)^2 - (1^2+2^2 +\cdots+n^2) \right\} \\ &=\frac{1}{2} \left\{ \left( \frac{1}{2}n(n+1) \right)^2 - \frac{1}{6}n(n+1)(2n+1) \right\} \\ &=\frac{1}{24}n(n+1) \{ 3n(n+1) - 2(2n+1) \} \\ &=\frac{1}{24}n(n+1)(3n^2 - n - 2) \\ &=\bm{\frac{1}{24}n(n+1)(n-1)(3n+2)} \end{align*}$

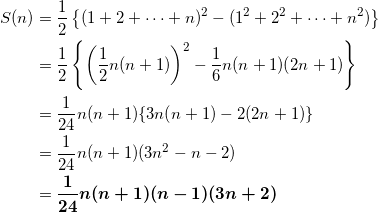
となる。

解説

計算のテクニック

　(2)、(3)では n や n + 1 という因数があらゆるところに出てくる計算を手早くする必要がある。この計算はコツを掴んでおくことが大事である。
　一度すべて展開してしまうと、複雑になり計算ミスを誘発するだけでなく、あとで因数分解するのが難しくなる。そこで、できるだけ因数を先にくくりだして、計算を楽に行うように計算を進めたい。これは数列のシグマの計算では必ず意識しておきたい。