空間内の4点
O ( 0 , 0 , 0 ) , A ( 0 , 2 , 3 ) , B ( 1 , 0 , 3 ) , C ( 1 , 2 , 0 )
を考える。このとき、以下の問いに答えよ。
(1) 4点 O , A , B , C を通る球面の中心 D の座標を求めよ。
(2) 3点 A , B , C を通る平面に点Dから垂線を引き、交点をFとする。線分DFの長さを求めよ。
(3) 四面体ABCDの体積を求めよ。
[2011 九州大・理]
イズミの解答への道
空間ベクトルの基本問題かつ頻出問題です。解答では普通の解き方を示しますので、この解き方は必ずできるようにしておきましょう。
別解として平面の方程式とベクトルの外積を用いた超高校級の解答を示しておきます。今回のようにピッタリはまる問題は少ないですが、高校で学ばない数学の世界を感じてもらえれば幸いです。
解答
(1) Dを ( a , b , c ) とすると、
a2 + b2 + c2 = a2 + ( b – 2 )2 + ( c – 3 )2
a2 + b2 + c2 = ( a – 1 )2 + b2 + ( c – 3 )2
a2 + b2 + c2 = ( a – 1 )2 + ( b – 2 )2 + c2
をそれぞれ整理すると、
4b + 6c = 13
2a + 6c = 10
2a + 4b = 5
であり辺々足して a , b , c を求めると、 ![]() となるので、求める座標は、
となるので、求める座標は、
![]()
となる。
(2) Fは![]() を含む平面上の点だから、
を含む平面上の点だから、
![]()
で表される。いま、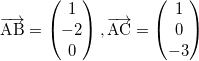 であるから、
であるから、
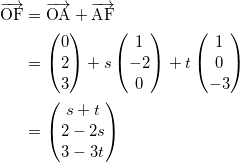
となるので、
![Rendered by QuickLaTeX.com \[ \overrightarrow{\text{DF}} = \overrightarrow{\text{OF}} - \overrightarrow{\text{OD}} =\begin{pmatrix} s+t-\frac{1}{2} \\ -2s+1 \\ -3t+\frac{3}{2} \end{pmatrix} \]](http://izu-mix.com/math/wp-content/ql-cache/quicklatex.com-1873335286c089fe2fdd9fe6d788dea0_l3.png)
となる。
ここで、![]() は、
は、![]() に垂直だから、
に垂直だから、![]() を満たす。すなわち、
を満たす。すなわち、
(a) 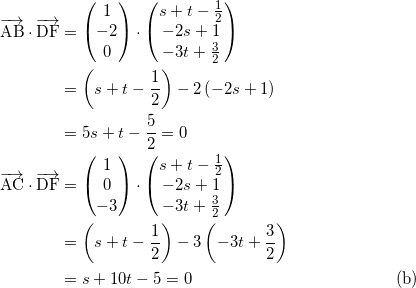
(a)、(b)を連立して、
![]()
となるので、
![Rendered by QuickLaTeX.com \[ \overrightarrow{\text{DF}} = \frac{3}{49} \begin{pmatrix} 6 \\ 3 \\ 2 \end{pmatrix} \]](http://izu-mix.com/math/wp-content/ql-cache/quicklatex.com-d56f3487d729d835de88cad44c2ede9f_l3.png)
であるから、
![]()
(3) △ABCの面積は、
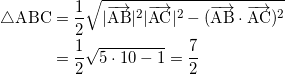
であるから、求める体積をVとすると、
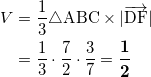
解説
超高校級の解法
ここでは、高校では学ばないベクトルの外積や、平面の方程式などを利用した超高校級の解答を示しましょう。知識についてはあとで補充します。まずは、(2)、(3)が驚くほど簡単に解けることを実感してください。
点 A , B , C を通る平面の法線ベクトルは、![]() の外積だから、
の外積だから、
![Rendered by QuickLaTeX.com \[ \overrightarrow{\text{AB}} \times \overrightarrow{\text{AC}} = \begin{pmatrix} 1 \\ -2 \\ 0 \end{pmatrix} \times \begin{pmatrix} 1 \\ 0 \\ -3 \end{pmatrix} = \begin{pmatrix} 6 \\ 3 \\ 2 \end{pmatrix} \]](http://izu-mix.com/math/wp-content/ql-cache/quicklatex.com-0f4ffb091dcccccd7c9cad747601c6ca_l3.png)
となる。よって点 A , B , C を通る平面の方程式は、
6x + 3y + 2z = k
となる。この平面の方程式αは点Aを通るので、k の値は、
k = 6・0 + 3・2 + 2・3 = 12
となる。よって、
6x + 3y + 2z – 12 = 0
である。
最後に、点と平面の距離の公式より、この平面と点Dとの距離DFは、
![]()
となる。
【ベクトルの外積】
2つのベクトルと
のどちらにも垂直なベクトルは、
で表される。これをベクトルの外積という。
【平面の方程式】
法線ベクトル(平面に直角なベクトル)が ( a , b , c ) であるような平面の方程式は、
ax + by + cz = k
で表される。
【平面と点の距離】
平面 ax + by + cz – k = 0 と 点( p , q , r ) の距離 d は
である。
前半の3つはセットで覚えましょう。平面と点の距離を求めるためには平面の方程式が必要ですが、平面の方程式を求めるには法線ベクトル(平面に直角なベクトル)が必要です。それを求めるのが外積です。
【四面体の体積】
3辺のベクトルが ( a , b , c ) , ( l , m , n ) , ( p , q , r ) で与えられる四面体の体積 V は、行列式を用いて、
で与えられる。

![Rendered by QuickLaTeX.com \[ \overrightarrow{p} \times \overrightarrow{q} = \begin{pmatrix} p_2 q_3 - p_3 q_2 \\ p_3 q_1 - p_1 q_3 \\ p_1 q_2 - p_2 q_1 \end{pmatrix} \]](http://izu-mix.com/math/wp-content/ql-cache/quicklatex.com-515a5e5221a67241e64513cf6aa0483e_l3.png)
![Rendered by QuickLaTeX.com \[ V = \frac{1}{6}\begin{vmatrix} a & l & p \\ b & m & q \\ c & n & r \end{vmatrix} = \frac{1}{6}(amr + lqc + pbn - anq - lbr - pmc ) \]](http://izu-mix.com/math/wp-content/ql-cache/quicklatex.com-1b8b33329696991213208a9c482b42f1_l3.png)
コメント