問題
図のように円に内接する四角形 ABCD において、![]() とし、∠ABC = α, ∠CDA = β とする。さらに
とし、∠ABC = α, ∠CDA = β とする。さらに![]() とするとき、次の空欄を埋めよ。
とするとき、次の空欄を埋めよ。
(1) ![]() を a , b , α を用いて表すと、
を a , b , α を用いて表すと、
![]()
(2) cosβ = -cosα の関係を用いて cosα を a , b , c , d で表すと、
![]()
となる。
(3) sin2α = ( 1 – cosα ) ( 1 + cosα ) なる関係、 sinα > 0 なることに注目すると、
![]()
となる。
(4) したがって、四角形の面積 T は、sinβ = sinα なので、
T = △ABC + △ADC =
となる。
イズミの解答への道
円に内接する四角形の面積を求める問題で、辺の値が具体的な値だったら、練習問題として何度も解いたハズの問題。指示に従って解いてみると、意外な結果が現れます。
とにかく指示に従って解けば、とりあえず穴は埋められるはずです。
解答
(1) △ABCにおいて余弦定理より、
AC2 = a2 + b2 – 2ab cosα
(2) △ADCにおいて余弦定理より、
AC2 = c2 + d2 – 2cd cosβ
= c2 + d2 + 2cd cosα
となり、これを(1)の結果と連立すると、
a2 + b2 – 2ab cosα = c2 + d2 + 2cd cosα
より、
![]()
(3)
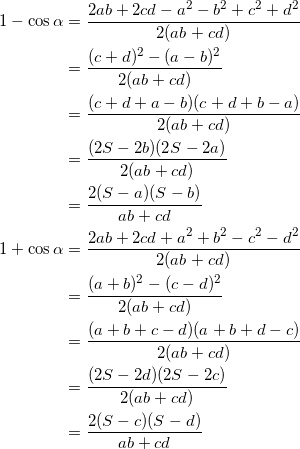
であるから、
![]()
となり、 sinα > 0 であるから、
![]()
である。
(4) sinβ = sinα であるから、
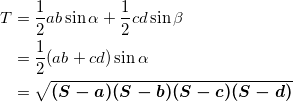
である。
研究
ブラーマグプタの公式
結果が非常に美しい。公式としてまとめておこう。
ブラーマグプタの公式
辺の長さがそれぞれ a , b , c , d である円に内接する四角形の面積 S は、
2s = a + b + c + d
とおいたとき、
![]()
で与えられる。
公式の形はヘロンの公式に非常に似ているので、覚えやすいもの。
教科書には載っていないので、これを公式として利用するのはあまりよくないのかもしれないが、検算や、時間がないときには威力を発揮する公式である。
なお、2002年の滋賀医大でもブラーマグプタの公式に関する問題が出題されている。

コメント