2018年センター数学IA 第1問[3]

2018年センター数学IA
　第1問[1]　第1問[2]　第1問[3]　第2問[1]　第2問[2]　第3問　第4問　第5問
　数学IA講評　PDF　>>数学IIB

　a を正の実数とし、
　　f ( x ) = ax² – 2 ( a + 3 ) x – 3a + 21
とする。2次関数 y = f ( x ) のグラフの頂点の x 座標を p とおくと
　　p = 　サ　 + 　シ　a
である。

　0 ≦ x ≦ 4 における関数 y = f ( x ) の最小値が f ( 4 ) となるような a の値の範囲は
　　0 < a ≦ 　ス　
である。
　また、 0 ≦ x ≦ 4 における y = f ( x ) の最小値が f ( p ) となるような a の値の範囲は
　　　セ　 ≦ a
である。
　したがって、 0 ≦ x ≦ 4 における関数 y = f ( x ) の最小値が 1 であるのは、
　　a = 　ソ　　タ　または a = 　タ　 + √　ツテ　　ト　
のときである。

解答

サシ

　与えられた式を平方完成すると、

$\begin{align*} f(x) &= ax^2 -2(a+3)x -3a+21 \\ &=a \left( x - \frac{a+3}{a} \right)^2 - \frac{(a+3)^2}{a} - 3a +21 \\ \end{align*}$

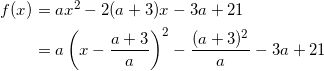
なので、頂点の x 座標は、

$p = \frac{a+3}{a} = \bm{1 + \frac{3}{a}}$

となる。

スセ

　グラフの形を考えます。 a < 0 より、頂点 $\displaystyle p = 1 + \frac{3}{a} > 0$ であるから、 x = 0 はグラフの左半分にあります。
　よって、0 ≦ x ≦ 4 における最小値は、その範囲が左半分に収まる場合は f ( 4 ) が最小値、範囲が頂点をこえる場合には頂点が最小値（ f ( p ) が最小値）となることが分かります。

　ここまでを考えて、最小値が x = 4 のときとなるためには、範囲の右端 x = 4 が頂点 x = p 以下であればよい。よって、

$\begin{align*} 4 &\leqq p \\ 1+ \frac{3}{a} &\geqq 4 \\ \frac{3}{a} &\geqq 3 \end{align*}$

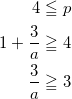
より、 3 ≧ 3a すなわち、( 0 < ) a ≦ 1 となる。

　同様に、最小値が f ( p ) となるためには、 p ≦ 4 であればよく、これは 1 ≦ a のときとなる。

ソタチツテト

　0 < a ≦ 1 のとき、最小値は

$\begin{align*} f(4) &= 16a - 2(a+3)\cdot 4 - 3a +21 \\ &=5a - 3 =1 \end{align*}$

を解いて、 $\displaystyle a = \bm{\frac{4}{5}}$ である。

　1 ≦ a のとき、最小値は

$f(p) = -\frac{(a+3)^2}{a} -3a +21 = 1$

を解いて、
　　( a + 3 )² + 3a² – 21a = -a
　　4a² -14a +9 = 0
より、
　　 $\displaystyle a = \frac{7 \pm \sqrt{49-36}}{4} = \frac{7 \pm \sqrt{13}}{4}$
となり、範囲より、 $\displaystyle a = \bm{\frac{7 + \sqrt{13}}{4}}$ となる。