△ABCにおいて、AB = 2 , AC = 1 , ∠A = 90° とする。
∠A の二等分線と辺BCの交点をDとすると、 ア √ イ ウ である。
点Aを通り点Dで辺BCに接する円と辺ABとの交点でAと個となるものをEとすると、AB・BE = エオ カ であるから、 BE = キク ケ である。
次の コ には下の⓪~②から、 サ には③・④から当てはまるものを一つずつ選べ。
BEBD コ ABBC であるから、直線ACと直線DEの交点は辺ACの端点 サ の側の延長上にある。
⓪ < ① = ② >
③ A ④ C
その交点をFとすると、CFAF = シ ス であるから、 CF = セ ソ である。したがって、BFの長さが求まり、CFAC = BFAB であることがわかる。
次の タ には下の⓪~③から当てはまるものを一つ選べ。
点Dは△ABFの タ 。
⓪ 外心である ① 内心である ② 重心である
③ 外心、内心、重心のいずれでもない
解答
アイウ
角の二等分線は、対辺をその角を為す2つの辺の比で分割する。
![]() より、
より、![]()
となる。
エオカキクケ
法べきの定理より、
![]()
であり、 AB = 2 より、 ![]() となる。
となる。
コ
ここまでで求めた値を具体的に代入して比較します。
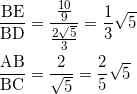
より、![]() となる。(よって、⓪が正解。)
となる。(よって、⓪が正解。)
サ
今の結果より、
![]()
となっているので、辺ACから点Bを高さ方向としてみたときに、Dの方が低い位置にあることがわかるので、直線EDは直線ACとCの延長線上の側で交わる。(よって、④が正解。)
シス
メネラウスの定理より、
![]()
より、
![]()
より、![]() である。
である。
セソ
今の結果から、
AC : CF = 3 : 5
である。いま、 AC = 1 なので、 ![]() となる。
となる。
タ
問題文にあるように、BA : BF = AC : FC となるので、線分BCは∠Bの二等分線となる。
つまり、点Dは∠Aの二等分線と∠Bの二等分線の交点となっており、点Dは△ABFの内心であるといえる。
なお、BD : DC ≠ 2 : 1 なので、 点Dは△ABFの重心ではない。
また、AD ≠ BD (もし AD = BD だとすれば、DはBCの中点にないといけないが、そうではない)なので、点Dは△ABFの外心でもない。
よって、点Dは△ABFの① 内心である。

コメント