2019年センター数学IA 第1問[3]

2019年センター数学IA
　第1問[1]　第1問[2]　第1問[3]　第2問[1]　第2問[2]　第3問　第4問　第5問
　数学IA講評　PDF　>>数学IIB

a と b はともに正の実数とする。 x の2次関数
　　y = x² + ( 2a – b ) x + a² + 1
のグラフをGとする。

(1)　グラフGの頂点の座標は
　　( b　チ　 – a , – b²　ツ　 + ab + 　テ　 )
である。

(2)　グラフ G が点 ( -1 , 6 ) を通るとき、 b のとり得る値の最大値は　ト　であり、そのときの a の値は　ナ　である。
　b = 　ト　 , a = 　ナ　のとき、グラフ G は2次関数 y = x² のグラフを x 軸方向に　ニ　　ヌ　、 y 軸方向に　ネノ　　ハ　だけ平行移動したものである。

解答

チツテ

　平方完成して、

$\begin{align*} y &= \left( x + \frac{2a-b}{2} \right)^2 - \left( \frac{2a-b}{2} \right)^2 + a^2 + 1 \\ &=\left\{ x - \left( \frac{2a-b}{2} \right) \right\}^2 - a^2 + ab - \frac{b^2}{4} + a^2 + 1 \end{align*}$

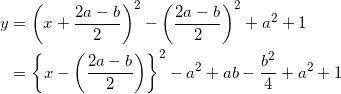
となるので、頂点の座標は、 $\displaystyle \left( \bm{\frac{b}{2} - a , -\frac{b^2}{4} + ab + 1 } \right)$ となる。

トナ

　グラフGが点 ( -1 , 6 ) を通るので、 x = -1 , y = 6 を代入して、
　　1 – ( 2a – b ) + a² + 1 = 6
　　a² – 2a + b = 4
　　( a – 1 )² + b = 5
と変形する。いま、 ( a – 1 )² = 5 – b ≧ 0 であるから、 b ≦ 5 となる。
　よって、 b の最大値は 5 で、このとき a = 1 である。

ニヌネノハ

　a = 1 , b = 5 のとき、頂点の座標は、

$\left( \frac{3}{2}, -\frac{25}{4} + 5 + 1 \right) = \left( \frac{3}{2} , -\frac{1}{4} \right)$

であるから、これは y = x² のグラフを、 x 方向に $\displaystyle \bm{\frac{3}{2}}$ 、 y 方向に $\displaystyle \bm{\frac{-1}{4}}$ 平行移動したグラフである。