2018年センター数学IIB 第3問

2018年センター数学IIB
　第1問[1]　第1問[2]　第2問　第3問　第4問
　数学IIB講評　PDF　>>数学IA

　第4項が30、初項から第8項までの和が288である等差数列を { a_n } とし、 { a_n } の初項から第 n 項までの和を S_n とする。また、第2項が36、初項から第3項までの和が156である等比数列で公比が1より大きいものを { b_n } とし、 { b_n } の初項から第 n 項までの和を T_n とする。

(1)　{ a_n } の初項は　アイ　、公差は　ウエ　であり
　　S_n = 　オ　 n² – 　カキ　 n
である。

(2)　{ b_n } の初項は　クケ　、公比は　コ　であり
　　T_n = 　サ　 ( 　シ　ⁿ – 　ス　 )
である。

解答

アイウエオカキ

　公差を d とすると、
　　a₁ = 30 – 3d , a₂ = 30 – 2d , … , a₇ = 30 + 3d , a₈ = 30 + 4d
であるから、
　　S₈ = 240 + 4d = 288
より、公差 d = 12 となり、初項 a₁ = 30 – 3・12 = -6 となる。

　一般項は、 a_n = -18 + 12n となるので、第n項までの和は、

$\begin{align*} S_n &= \sum_{k=1}^n (12k-18) \\ &=12 \times \frac{1}{2}n(n+1) -18n \\ &=\bm{6n^2 - 12n} \end{align*}$

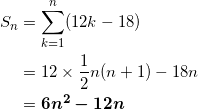
となる。

a₃ + a₅ = 2a₄ ,a₂ + a₆ = 2a₄ , a₁ + a₇ = 2a₄ などより、
　　S₈ = ( a₁ + a₇ ) + (a₂ + a₆) +( a₃ + a₅ ) + a₄ + a₈
　　= 7a₄ + a₈
　　= 7a₄ + ( a₄ + 4d )
　　= 8a₄ +4d
と求めています。

クケコサシス

　公比を r とすると、

$\frac{36}{r} + 36 + 36r = 156$

より、

$36r^2 - 120r + 36 = 0$

を解いて、 $\displaystyle r = \frac{1}{3} , 3$ 。条件より公比 r > 1 より、 r = 3 で、このとき初項 b₁ = 12 である。

　第n項までの和は公式より、

$T_n = \frac{b_1 (1-r^n)}{1-r} = \bm{6 ( 3^n -1 )}$

となる。

セ

　ちょっと様子を見てみます。問題文にある式を使うと、
　　d₁ = c₂ – c₁ = ( a₁ – b₁ ) + ( a₂ – b₂ )
　　d₂ = c₃ – c₂ = ( a₁ – b₁ ) + ( a₂ – b₂ ) + ( a₃ – b₃ )
となることから、
　　d_n = ( a₁ + a₂ + … + a_n+1 ) – ( b₁ + b₂ + … + b_n+1 )
　　　　= S_n+1 – T_n+1
となるので、答えは ⑤ となる。

厳密な計算をせず、いくつかの例から推測される結果で答えを導いてしまえば良い問題が、たまに出題されます。これはその問題といっていいでしょう。

ソタチ

　ここからは計算するだけです。

$\begin{align*} d_n &= 6(n+1)^2 -12(n+1) - 6(3^{n+1} -1 ) \\ &= 6n^2 - 6 - 2 \cdot 2^{n+2} + 6 \\ &= \bm{6}n^2 - 2 \cdot \bm{3}^{n+\bm{2}} \end{align*}$

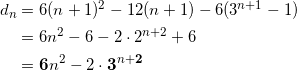
となる。

ツテト

　c₁ = a₁ – b₁ = -6 – 12 = -18 です。

ナニヌネ

　階差数列の公式に当てはめて計算するだけです。 n ≧ 2 において、

$\begin{align*} c_n &= c_1 + \sum_{k=1}^{n-1} d_k \\ &=-18 + 6 \cdot \frac{1}{6}n(n-1)(2n-1) - 2 \frac{3^3(1-3^{n-1})}{1-3} \\ &=-18 + n(n-1)(2n-1) + 3^3 - 3^{n+2} \\ &=\bm{2n^3 -3n^2 + n + 9 -3^{n+2}} \end{align*}$

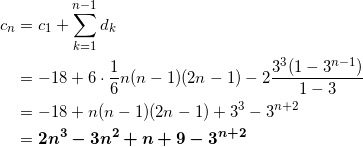
となる（これは n = 1 のときも成立）。