問題
(1) 0 ≦ θ ≦ 2π のとき
……① ![]()
となるθの値の範囲を求めよう。
加法定理を用いると、
![]() = √ ア イ cosθ + ウ イ sinθ
= √ ア イ cosθ + ウ イ sinθ
である。よって、三角関数の合成を用いると、①は、
sin ( θ + π エ ) < 0
と変形できる。したがって、求める範囲は
オ カ π < θ < キ ク π
である。
(2) 0 ≦ θ ≦ π2 とし、 k を実数とする。 sinθ と cosθ は x の2次方程式 25x2 ケコ であることがわかる。
さらに、θが sinθ ≧ cosθ を満たすとすると、sinθ = サ シ , cosθ = ス セ である。このとき、θは ソ を満たす。 ソ に当てはまるものを、次の ⓪ ~ ⑤ のうちから一つ選べ。
⓪ 0 ≦ θ < π12 ① π12 ≦ θ < π6 ② π6 ≦ θ < π4
③ π4 ≦ θ < π3 ④ π3 ≦ θ < 512π ⑤ 512π ≦ θ < π2
解答
アイウ
加法定理より、
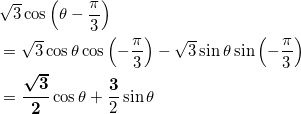
である。
エ
求める不等式は、
![]()
すなわち、
![]()
であり、左辺は三角関数の合成で変形すると、
![]()
となる。
オカキク
この不等式を解くと、
![]()
よって、
![]()
である。
ケコ
解と係数の関係より、
sinθ + cosθ = 3525 = 75
sinθcosθ = k25
となる。1つ目の式を両辺2乗して整理すると、
1 + 2sinθcosθ = 4925
より、
2k25 = 2425
より、 k = 12 である。
サシスセ
25x2 -35x + 12 = 0
( 5x – 3 ) ( 5x – 4 ) = 0
より、 x = 35 , 45 であり、sinθ ≧ cosθ であるから、
sinθ = 45 , cosθ = 35
である。
いま、sinθは、0 ≦ θ ≦ π2 の範囲で単調増加なので、
sinπ4 < sinθ < sinπ3
となることより、③ π4 ≦ θ < π3 である。

コメント