2021年共通テスト数学IA 第1問[1]

2021年共通テスト数学IA　>>数学IIB
講評　第1問[1]　第1問[2]　第2問[1]　第2問[2]　第3問　第4問

　cを正の整数とする。xの2次方程式
　　2x² + ( 4c – 3 ) x + 2c² – c – 11 = 0……①
について考える。

(1)　c = 1 のとき、①の左辺を因数分解すると
　　( 　ア　 x + 　イ　 ) ( x – 　ウ　 )
であるから、①の解は
　　x = 　イ　　ア　 , 　ウ　　
である。

(2)　c = 2 のとき、①の解は
　　x = – 　エ　 ± √　オカ　　キ　
であり、大きい方の解をαとすると
　　5α = – 　ク　 ± √　ケコ　　サ　
である。

　また、 m < 5α < m + 1 を満たす整数 m は　シ　である。

(3)　太郎さんと花子さんは、①の解について考察している。

太郎：①の解は c の値によって、ともに有理数である場合もあれば、ともに無理数である場合もあるね。c がどのような値のときに、解は有理数になるのかな。

花子：2次方程式の解の公式の根号の中に着目すればいいんじゃないかな。

　①の解が異なる二つの有理数であるような正の整数 c の個数は　ス　個である。

解答

アイウ

　c = 1 のとき、
　　①の左辺 = 2x² + x – 10
　　　　　= ( 2x + 5 ) ( x – 2 )

エオカキ

　c = 2 のとき、①は
　　2x² + 5x – 5 = 0
であり、解の公式より、

$x = \frac{-5 \pm \sqrt{5^2 - 4 \cdot 2 \cdot (-5)}}{2 \cdot 2} = \frac{\bm{-5} \pm \sqrt{\bm{65}}}{\bm{4}}$

である。

クケコサ

　大きい方の解αは、

$\alpha = \frac{-5 + \sqrt{65} }{4}$

である。求める値は、分母の有理化によって、

$\begin{align*} \frac{5}{\alpha} &= 5 \times \frac{4}{-5 + \sqrt{65}} \\ &= 5 \times \frac{4(-5-\sqrt{65})}{25 - 65} \\ &=\frac{\bm{5}+\sqrt{\bm{65}}}{\bm{2}} \end{align*}$

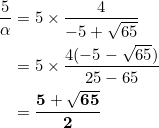
となる。

シ

　8 < √65 < 9 であることから、

$4 < \frac{\sqrt{65}}{2} < 4.5$

より、

$6 < 4+2.5 < \frac{5+\sqrt{65}}{2} < 4.5+ 2.5 = 7$

より、求める m は m = 6 である。

ス

　①を解の公式で解いたときの根号の中身は、
　　( 4c – 3 )² – 4・2・(2c² – c – 11 ) = 97-16c ( = M とおく)
であり、これが平方数になっていればよい。
　この数が負になることはないので、限りがあるので、以下書き出して数える。
　　c = 1 のとき M = 81（平方数）より、解は有理数になる
　　c = 2 のとき M = 65 となるので、解は無理数
　　c = 3 のとき M = 49（平方数）より、解は有理数になる
　　c = 4 のとき M = 33 となるので、解は無理数
　　c = 5 のとき M = 17 となるので、解は無理数
　　c = 6 のとき M = 1（平方数）より、解は有理数になる
ことから、解が有理数になる正の整数の個数は 3 つ。