第2問
解答
アイウエ
平均変化率は公式通りで、
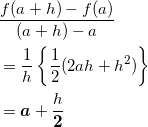
となる。これより、
![]()
となる。
オカ
接線 l も公式通りで、
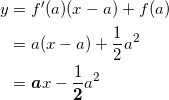
である。
キク
この直線 l と x 軸の交点は、 y = 0 との連立方程式
![]()
を解いて、![]() であるから、交点の座標は
であるから、交点の座標は![]() である。
である。
ケコサシス
求める直線 m は、直線 l と直交することより傾きは ![]() であり、今求めた交点
であり、今求めた交点![]() を通るので、
を通るので、
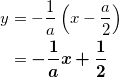
セソ
Aの座標は、直線 m に x = 0 を代入して y = 1/2 より、A ( 0 , 1/2 ) 。
求める面積は
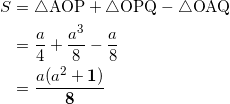
タチツ
次に面積 T について考える。 P から x 軸におろした垂線の足を R としたとき、
![Rendered by QuickLaTeX.com \begin{align*} T&=\triangle \text{AOP} + \triangle \text{POR} - \int_0^a \frac{1}{2}x^2 dx \\ &= \frac{a}{4} + \frac{a^3}{4} - \left[ \frac{1}{6} x^3 \right]_0^a \\ &=\frac{a}{4} + \frac{a^3}{4} - \frac{a^3}{6} \\ &=\frac{a^3+ 3a}{12} \\ &=\frac{a (a^2 + \bm{3})}{\bm{12}} \end{align*}](http://izu-mix.com/math/wp-content/ql-cache/quicklatex.com-83b5289f1340f7022797fb864cb3b4b8_l3.png)
である。
テトナ
ここは計算をするだけである。
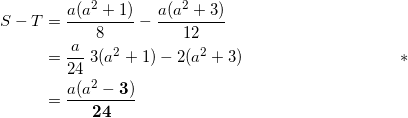
二
題意にそって、![]() であることを考えると、 S – T > 0 となるのは、 a2 – 0 > 0 のとき、すなわち
であることを考えると、 S – T > 0 となるのは、 a2 – 0 > 0 のとき、すなわち![]() のときである。
のときである。
ヌネノハヒ
極値を与えるのは微分した関数が 0 となる点。いま、
![]()
とすると、
![]()
であり、![]() となるのは
となるのは![]() のときであり、増減表より
のときであり、増減表より![]() のとき最小値を与える。
のとき最小値を与える。
よって、最小値は、![]() のとき、
のとき、
![]()
である。

コメント
最後のヌネノハヒの部分の答えですが,
一番最後:g(1)=-1/12だと思います.
>yun.morisさん
ご指摘のとおりです、修正しておきます。