第3問
解答
アイウエオ
2nは、
2, 4, 8, 16, 32, …
と増えていくので、その一の位の数を取った数列 { an } は、
a1 = 2,
a2 = 4,
a3 = 8,
a4 = 6,
a5 = 2,
となる。周期が 4 で繰り返される循環数列であるから、
an+4 = an
が成り立つ。
カ
問題文にある通り、?を繰り返し用いることで、
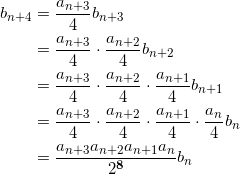
となる。
キ
ここは数学的な勘を働かせないと(教科書通りでは)難しい。
いま、{ an } は周期 4 の循環数列なので、連続する4項の積は、どの連続する4項でも同じである。よって、
an+3 an+2 an+1 an
=a4 a3 a2 a1
=2・4・8・6
=3・27
となる。
クケ
これを代入して、
![]()
が成り立つ。
コサシスセソ
いま見たように、数列 { bk } は、
![]()
を満たし、またその初めの4項は、
![]()
である。
ここで、たとえば { b4k-3 } は、 b1, b5, b9, … という数列であり、これは初項 b1 = 1 、公比 ![]() の等比数列である。よってその一般項は、
の等比数列である。よってその一般項は、
![]()
となる。
同様に、{ b4k-2 }は初項 ![]() 、公比
、公比 ![]() の等比数列だから、
の等比数列だから、
![]()
であり、{ b4k-1 }は初項 ![]() 、公比
、公比 ![]() の等比数列だから、
の等比数列だから、
![]()
となり、{ b4k }は初項 ![]() 、公比
、公比 ![]() の等比数列だから、
の等比数列だから、
![]()
となる。
タチ
いま、
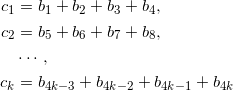
のようにおくと、求める値は、
![]()
となる。いま、
![]()
であり、
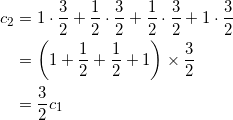
であり、同様に考えて、
![]()
が成り立つことがわかる。
以上より、求める値は、初項![]() 、公比
、公比![]() の等比数列の初項から第 m 項までの和であるから、公式より、
の等比数列の初項から第 m 項までの和であるから、公式より、
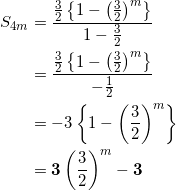
となる。
ツテ
同様に、
![]()
とおくと、
![]()
であり、
![]()
となり、同様に、
![]()
であるから、
![Rendered by QuickLaTeX.com \[ d_i = \frac{1}{4} \left\{ \left( \frac{3}{2} \right)^4 \right\}^{i-1} \]](http://izu-mix.com/math/wp-content/ql-cache/quicklatex.com-dc85c6ab0bf713272c54fe5177a0b407_l3.png)
が成り立つ。よって、
![]()
となる。
トナ
求める値は、
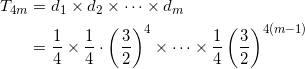
である。この積について、
 は m 個含まれる
は m 個含まれる
 は、
は、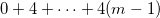 個含まれる。
個含まれる。
ここで、この個数は初項 0 、末項 4(m-1) 、項数 m の等差数列の和であるから、![Rendered by QuickLaTeX.com \[ m \times \frac{4m-4}{2} = 2m^2 - 2m \]](http://izu-mix.com/math/wp-content/ql-cache/quicklatex.com-6e5fe09c12c23bcdf1d932e9da869976_l3.png)
である。
よって、
![]()
となる。
ニヌネ
![]() を求める。問題文にあるように
を求める。問題文にあるように![]() は自然数だったので、先ほどの式に
は自然数だったので、先ほどの式に![]() を代入するわけにも行かないので、地道に計算する。
を代入するわけにも行かないので、地道に計算する。
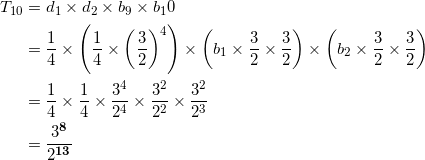

コメント