第1問[1]
解答
アイウエオカキ
2点間の距離の公式を用いて求める。
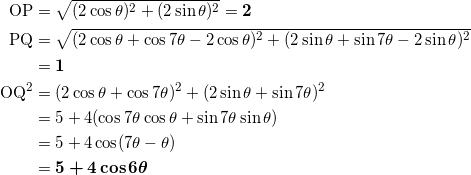
である。
いま、![]() であるから、
であるから、
![]()
であるから、
![]()
となり、 OQ が最大値を取るのは、 cos 6θ = 0 すなわち ![]() のとき、最大値は
のとき、最大値は![]() である。
である。
ク
いま、2点は、O ( 0 , 0 ), P ( 2cosθ, 2sinθ ) であるから、この2点を通る直線は、傾きが ![]() で、原点を通る1次関数だから、
で、原点を通る1次関数だから、
![]()
すなわち、
![]()
ケ
直線OQの傾きが、直線OPの傾きと等しければよいので、
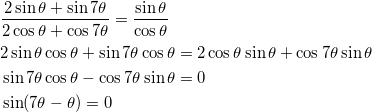
より、 sin 6θ = 0 より、
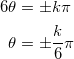
このうち、![]() を満たすのは、 k = 1 のときであるから、
を満たすのは、 k = 1 のときであるから、![]() であればO、P、Qは一直線上に並ぶ。
であればO、P、Qは一直線上に並ぶ。
コサシ
いま、条件よりOQPが90°であり、OP = 2 , PQ = 1 であるから、△OPQにおいて三平方の定理より
![]()
である。このとき、
![]()
を解いて、
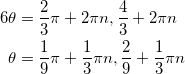
であるが、このうち、![]() を満たすのは、
を満たすのは、
![]()
のときである。

コメント