第1問[2]
解答
スセソタチツテ
与えられた式の両辺を、1つ目の式は2乗、2つ目の式は3乗すると、
(a) ![]()
(b) ![]()
となる。ここで、![]() を計算すると、
を計算すると、
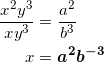
となる。
さらに、与えられた2つ目の式より、
![]()
であるから、ここに x を代入して、
![]()
となる。
トナニ
![]() より、
より、
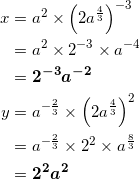
である。
ヌネノハ
問題文の誘導に乗る。相加相乗平均の関係式
![]()
より、いま、
![]()
が成り立つ。またこの不等式の等号が成り立つのは x = y のとき、すなわち、
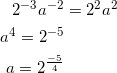
のときである。
以上のことより、 x + y は、![]() のとき、最小値
のとき、最小値![]() をとる。
をとる。

コメント