(1) 1ラジアンとは、 ア のことである。 ア に当てはまるものを、次の⓪~③のうちから一つ選べ。
⓪ 半径が1、面積が1の扇形の中心角の大きさ
① 半径がπ、面積が1の扇形の中心角の大きさ
② 半径が1、弧の長さが1の扇形の中心角の大きさ
③ 半径がπ、弧の長さが1の扇形の中心角の大きさ
(2) 144°を弧度で表すと イ ウ πラジアンである。また、 ![]() ラジアンを度で表すと エオカ °である。
ラジアンを度で表すと エオカ °である。
(3) ![]() の範囲で
の範囲で
① ![]()
を満たす θ の値を求めよう。
![]() とおくと、①は
とおくと、①は
2 sin x – 2 cos ( x – π キ ) = 1
と表せる。加法定理を用いると、この式は
sin x – √ ク cos x = 1
となる。さらに、三角関数の合成を用いると
sin ( x – π ケ ) = 1 コ
と変形できる。 ![]() だから、 θ = サシ スセ π である。
だから、 θ = サシ スセ π である。
解答
ア
1ラジアンとは、弧の長さが半径と同じになるような扇形の中心角の大きさなので、②が適当。
イウエオカ
180° = π ラジアンというところから考えましょう。
144°は ![]() ラジアン。
ラジアン。
![]() より、345°。
より、345°。
キ
![]()
であるから、
(※) ![]()
となる。
ク
加法定理より、
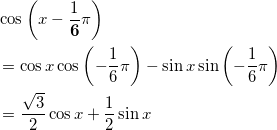
となるので、(※)式を変形して、
![]()
となる。
ケコ
さらに三角関数の合成の公式より、
![]()
すなわち、
(※※) ![]()
となる。
サシスセ
(※※)式を解くと、整数 k を用いて
![]()
となるので、
![]()
であり、さらにθに直して、
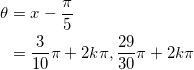
となり、![]() より、
より、![]() となる。
となる。

コメント