2020年センター数学IIB 第1問[2]

問題

(1)　tは正の実数であり、 $\displaystyle t^{\frac{1}{3}} - t^{-\frac{1}{3}} = -3$ を満たすとする。このとき、
　　 $\displaystyle t^{\frac{2}{3}} + t^{-\frac{2}{3}} =$ 　タチ　
である。さらに
　　 $\displaystyle t^{\frac{1}{3}} + t^{-\frac{1}{3}} =$ √　ツテ　 , t – t^-1 = 　トナニ　
である。

(2)　x , y は正の実数とする。連立方程式

……② $\log_3 ( x\sqrt{y} ) \leqq 5$

……③ $\log_{81} \frac{y}{x^3} \leqq 1 \\$

について考える。
　X = log₃ x , Y = log₃ y とおくと、②は
　　　ヌ　 X + Y ≦ 　ネノ　……④
と変形でき、③は
　　　ハ　 X – Y ≦ 　ヒフ　……⑤
と変形できる。
　X , Y が④と⑤を満たすとき、Y のとり得る最大の整数の値は　ヘ　である。また、 x , y が②、③と log₃ y = 　ヘ　を同時に満たすとき、 x のとり得る最大の整数の値は　ホ　である。

解答

タチ

　そのまま解いてもよいが、分かりやすくするために $\displaystyle t^{\frac{1}{3}} = a$ とおいて考える。すると問題の式は、
　　a – 1a = -3
である。これを辺々2乗すると、
　　a² – 2・a・1a + 1a² = 9
　　a² + 1a² = 9 + 2 = 11
である。

ツテ

　次に求めるのは、x = a + 1a ( > 0 ) の値である。
　両辺2乗すると、
　　x² = a² + 2 + 1a²
であり、先程の結果から a² + 1a² = 11 を代入すると、
　　x² = 11 + 2
すなわち、求める値は、 x = √13 である。

トナニ

　求める値は a³ – 1a³ の値である。
　問題文に与えられた式
　　a – 1a = -3
を辺々3乗して、
　　a³ – 3a²・1a + 3a・1a² – 1a³ = -27
　　a³ – 3a + 3・1a – 1a³ = -27
　　a³ – 3 ( a –1a ) – 1a³ = -27
より、問題で与えられた式の数値を代入して、
　　a³ – 1a³ = -27 + 3・(-3) = -36
となる。

ヌネノ

　与えられた式を変形して、

$\begin{align*} &\log_3 x\sqrt{y} \leqq 5 \\ &\log_3 x + \log_3 \sqrt{y} \leqq 5 \\ &\log_3 x + \frac{1}{2} \log_3 y \leqq 5 \end{align*}$

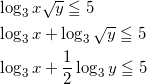
より、 2X + Y ≦ 10 である。

ハヒフ

　底の変換公式を利用して、

$\begin{align*} &\log_{81} \frac{y}{x^3} \leqq 1 \\ &\frac{\log_3 y}{\log_3 81} - 3 \cdot \frac{\log_3 x}{\log_3 81} \leqq 1 \\ &\frac{1}{4}Y - \frac{3}{4} X \leqq 1 \end{align*}$

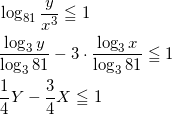
を整理して、 3X – Y ≧ -4 である。

ヘ

　XY軸で④、⑤の条件を満たす領域を描くと以下の通りになる。
　図より、Yがとり得るの最大の整数は、 Y = 7 となる。

ホ

　図より Y = 7 を満たす X の範囲は、1 ≦ X ≦ 32 であるから、
　　3 ≦ x ≦ $3^{\frac{3}{2}}$ = √27
となる。これを満たす最大の整数 x = 5 である。