解答
アイウエオカ
公式通り計算して、
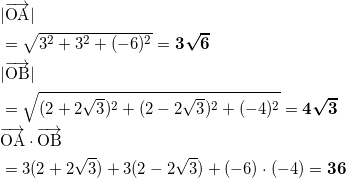
キクケコ
問題文にある通り ![]() とおくと、
とおくと、
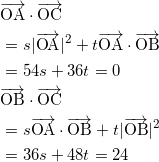
である。1つ目の式から、 t = – 32 s となるので、これを2つ目の式に代入して、
36s – 72s = 24
より、
s = -23
であり、これより
t = 1
となる。
サシ
以上の結果より、![]() であるから、
であるから、
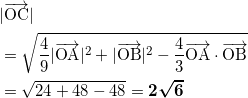
となる。
スセソタ
![]() であるから、
であるから、
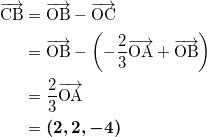
となる。
チ
今の結果より、OA//CBであるが、OA≠CBであることがいえる。
つまり、1組の辺が平行で長さは異なるような四角形なのでこれは台形である。また平行四辺形にはならない。よって、
③ 平行四辺形ではないが台形である
が正解。
ツテ
問題文にある通り、![]() ⊥
⊥![]() であるから、求める面積は、
であるから、求める面積は、
四角形OABC = ( OA + CB ) × OC × 12
= 5√6 × 2√6 × 12 = 30
である。
トナニヌネノ
点D の座標を D ( p , q , 1 ) とおく。このとき、
![]()
であり、
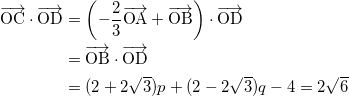
となる。(途中で、![]() を使用した。)
を使用した。)
これらの方程式を解いて、
p = √22 + 1
q = 1 – √22
となる。
ハヒ
![Rendered by QuickLaTeX.com \[ \cos \angle \text{COD} = \frac{\overrightarrow{\text{OC}} \cdot \overrightarrow{\text{OD}}}{|\overrightarrow{\text{OC}}||\overrightarrow{\text{OD}}|} = \frac{2\sqrt{6}}{2\sqrt{6} \cdot 2} = \frac{1}{2} \]](http://izu-mix.com/math/wp-content/ql-cache/quicklatex.com-277ed8d4b75d3f7a792289bcb23a70f6_l3.png)
より、 ∠COD = 60°
フ
図を書いて考える。Dから直線OC上へ下ろした垂線の足をHとすると、△ODH はODを斜辺とする直角三角形なので、 DH = √3 となる。
ヘホ
四面体DABC = △ABC × DH × 13
である。
△ABC = 2√6 × 2√6 × 12 = 12
であるから、
四面体DABC = 12 × √3 × 13 = 4√3
となる。

コメント