2022年共通テスト数学IIB 第5問

2022年共通テスト数学IIB　>>数学IA
講評　第1問[1]　第1問[2]　第2問[1]　第2問[2]　第4問　第5問

　平面上の点 O を中心とする半径 1 の円周上に 3 点 A , B , C があり、 $\displaystyle \overrightarrow{\text{OA}} \cdot \overrightarrow{\text{OB}} = -\frac{2}{3}$ および $\overrightarrow{\text{OC}} = - \overrightarrow{\text{OA}}$ を満たすとする。 t を 0 < t < 1 を満たす実数とし、線分 AB を t : ( 1 – t ) に内分する点を P とする。また、直線 OP 上に点 Q をとる。

(1)　cos∠AOB = 　アイ　　ウ　である。
　また、実数 k を用いて $\overrightarrow{\text{OQ}} = k \overrightarrow{\text{OP}}$ と表せる。したがって
　　 $\overrightarrow{\text{OQ}}$ = 　エ　 $\overrightarrow{\text{OA}}$ + 　オ　 $\overrightarrow{\text{OB}}$ ……①
　　 $\overrightarrow{\text{CQ}}$ = 　カ　 $\overrightarrow{\text{OA}}$ + 　キ　 $\overrightarrow{\text{OB}}$
となる。
　 $\overrightarrow{\text{OA}}$ と $\overrightarrow{\text{OP}}$ が垂直になるのは、 t = 　ク　　ケ　のときである。

　エ　～　キ　の解答群（同じものを繰り返し選んでもよい。）

⓪　kt　　①　( k – kt )　　②　( kt + 1 )
③　( kt – 1 )　　④　( k – kt + 1 )　　⑤　( k – kt – 1 )

　以下、 t ≠ 　ク　　ケ　とし、∠OCQ が直角であるとする。

(2)　∠OCQ が直角であるとことにより、(1)の k は
　　k = 　コ　　サ　 t – 　シ　……②
となることがわかる。

　平面から直線 OA を除いた部分は、直線OAを境に二つの部分に分けられる。そのうち、点 B を含む部分を D₁ 、含まない部分を D₂ とする。また、平面から直線 OB を除いた部分は、直線 OB を境に二つの部分に分けられる。そのうち、点 A を含む部分を E₁ 、含まない部分を E₂ とする。

0 < t < 　ク　　ケ　ならば、点 Q は　ス　。
　ク　　ケ　 < t < 1 ならば、点Q は　セ　。

　ス　、　セ　の解答群（同じものを繰り返し選んでもよい。）

⓪　D₁ に含まれ、かつ E₁ に含まれる
①　D₁ に含まれ、かつ E₂ に含まれる
②　D₂ に含まれ、かつ E₁ に含まれる
③　D₂ に含まれ、かつ E₂ に含まれる

(3)　太郎さんと花子さんは、点 P の位置と $|\overrightarrow{\text{OQ}}|$ の関係について考えている。 t = 12 のとき、①と②より、 $|\overrightarrow{\text{OQ}}|$ = √　ソ　とわかる。

太郎： $\displaystyle t \neq \frac{1}{2}$ のときにも $|\overrightarrow{\text{OQ}}|$ = √　ソ　となる場合があるかな。

花子： $|\overrightarrow{\text{OQ}}|$ を t を用いて表して、 $|\overrightarrow{\text{OQ}}|$ = √　ソ　を満たす t の値について考えればいいと思うよ。

太郎：計算が大変そうだね。

花子：直線 OA に関して $\displaystyle t = \frac{1}{2}$ のときの点 Q と対称な点を R としたら、 $|\overrightarrow{\text{OQ}}|$ = √　ソ　となるよ。

太郎： $\overrightarrow{\text{OR}}$ を $\overrightarrow{\text{OA}}$ と $\overrightarrow{\text{OB}}$ を用いて表すことができれば、 t の値が求められそうだね。

　直線 OA に関して、 t = 12 のときの点 Q と対称な点を R とすると
　　 $\overrightarrow{\text{CR}}$ = 　タ　 $\overrightarrow{\text{CQ}}$
　　　　　= 　チ　 $\overrightarrow{\text{OA}}$ + 　ツ　 $\overrightarrow{\text{OB}}$
となる。
　t ≠ 12 のとき $|\overrightarrow{\text{OQ}}|$ = √　ソ　となる t の値は　テ　　ト　である。

解答

アイウ

　A , B , C は半径 1 の円周上にあるので、 $| \overrightarrow{\text{OA}} | =| \overrightarrow{\text{OB}} | = | \overrightarrow{\text{OC}} | = 1$ である。内積の定義より、

$\overrightarrow{\text{OA}} \cdot \overrightarrow{\text{OB}} = | \overrightarrow{\text{OA}} | | \overrightarrow{\text{OB}} | \cos \angle \text{AOB} = -\frac{2}{3}$

より、 cos∠AOB = -23

エオカキ

　点Pの定義より、

$\overrightarrow{\text{OP}} = t\overrightarrow{\text{OB}} + ( 1 -t) \overrightarrow{\text{OA}}$

だから、

$\begin{align*} \overrightarrow{\text{OQ}} &= k\overrightarrow{\text{OP}} \\ &= \bm{(k-kt)} \overrightarrow{\text{OA}} + \bm{kt} \overrightarrow{\text{OB}} \end{align*}$

である。
　また、 $\overrightarrow{\text{CO}} = -\overrightarrow{\text{OC}} = \overrightarrow{\text{OA}}$ であるから、

$\begin{align*} \overrightarrow{\text{CQ}} &= \overrightarrow{\text{CO}} + \overrightarrow{\text{OQ}} \\ &= \overrightarrow{\text{OA}} + (k-kt) \overrightarrow{\text{OA}} + k \overrightarrow{\text{OB}} \\ &= \bm{(k-kt+1)} \overrightarrow{\text{OA}} + \bm{kt} \overrightarrow{\text{OB}} \end{align*}$

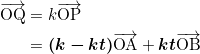
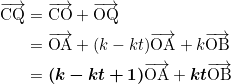
である。これを式③としておく。

クケ

　 $\overrightarrow{\text{OP}} = t\overrightarrow{\text{OB}} + ( 1 -t) \overrightarrow{\text{OA}}$ より、

$\overrightarrow{\text{OA}} \cdot \overrightarrow{\text{OP}} = t \overrightarrow{\text{OA}} \cdot \overrightarrow{\text{OB}} + ( 1-t) |\overrightarrow{\text{OA}}|^2 = 0$

より、
　　- 23 t + ( 1 – t ) = 0
を解いて t = 35 である。

コサシ

　　 $\overrightarrow{\text{CO}} = -\overrightarrow{\text{OC}} = \overrightarrow{\text{OA}}$
　　 $\overrightarrow{\text{CQ}} = (k-kt+1) \overrightarrow{\text{OA}} + k \overrightarrow{\text{OB}}$
であるから、

$\overrightarrow{\text{CO}} \cdot \overrightarrow{\text{CQ}} = \overrightarrow{\text{OA}} \cdot \{ (k-kt+1) \overrightarrow{\text{OA}} + k \overrightarrow{\text{OB}} \} = 0$

を整理して、
　　( k – kt + 1 ) – 23 kt = 0
となるので、これを k について解いて、
　　k = 35t – 3
である。

スセ

　t = 35 のときの図は以下のようになっている。

　よって、 t が 0 < t < 35 の範囲にあるときは、直線 OP は以下の図のようになるので、点 Q は領域 D₂ 、領域 E₂ に含まれる。よって③が正解。

　また、 t が 35 < t < 1 の範囲にあるときは、直線 OP は以下の図のようになるので、点 Q は領域 D₁ 、領域 E₁ に含まれる。よって⓪が正解。

ソ

　t = 1/2 を式②に代入して、 k = -6 である。これらを式①に代入すると、

$\overrightarrow{\text{OQ}} =-3 ( \overrightarrow{\text{OA}} + \overrightarrow{\text{OB}} )$

となるので、

$|\overrightarrow{\text{OQ}}|^2 = 9 ( 1 + 1 - 2 \cdot \frac{2}{3} ) = 6$

であるから、 OQ = √6 となる。

タチツ

　点 R は、t = 1/2 のときの、点Qを直線OAに関する対称な点であるから、

$\overrightarrow{\text{CR}} = \bm{-}\overrightarrow{\text{CQ}}$

である。式③に、 t = 1/2 , k = – 6 を代入して、

$\overrightarrow{\text{CR}} = \bm{2} \overrightarrow{\text{OA}} + \bm{3} \overrightarrow{\text{OB}}$

となる。

テト

　誘導にある通り、 $\overrightarrow{\text{OR}}$ を求めると、

$\overrightarrow{\text{OR}} = \overrightarrow{\text{OC}} + \overrightarrow{\text{CR}} = \overrightarrow{\text{OA}} + 3\overrightarrow{\text{OB}}$

となる。
　直線ABと直線ORの交点を P とすると、

$\overrightarrow{\text{OR}} = l \overrightarrow{\text{OP}} = lt \overrightarrow{\text{OB}} + l(1-t) \overrightarrow{\text{OA}}$

であるから、
　　lt = 3 , l ( 1 – t ) = 1
となるので、これを解いて l = 4 , t = 34 となる。

$\overrightarrow{\text{OR}} = \overrightarrow{\text{OA}} + 3\overrightarrow{\text{OB}} = 4 \times \dfrac{\overrightarrow{\text{OA}} + 3\overrightarrow{\text{OB}}}{4}$ という式変形ができれば、これだけで t = 3/4 が明らかである。この式変形はできるようにしておきたい。