2022年共通テスト数学IIB 第2問[2]

2022年共通テスト数学IIB　>>数学IA
講評　第1問[1]　第1問[2]　第2問[1]　第2問[2]　第4問　第5問

　b > 0 とし、 g ( x ) = x³ – 3bx + 3b² , h ( x ) = x³ – x² + b² とおく。座標平面上の曲線 y = g ( x ) を C₁ 、曲線 y = h ( x ) を C₂ とする。

　C₁ と C₂ は 2 点で交わる。これらの交点の x 座標をそれぞれ α , β ( α < β ) とすると、α = 　サ　 , β = 　シス　である。

　α ≦ x ≦ β の範囲で C₁ と C₂ で囲まれた図形の面積を S とする。また、 t > β とし、 β ≦ x ≦ t の範囲で C₁ と C₂ および直線 x = t で囲まれた図形の面積を T とする。
　このとき
　　S = $\displaystyle \int_{\alpha}^{\beta}$ 　セ　 dx
　　T = $\displaystyle \int_{\beta}^{t}$ 　ソ　 dx
　　S – T = $\displaystyle \int_{\alpha}^{t}$ 　タ　 dx
であるので
　　S – T = 　チツ　　テ　 ( 2t³ – 　ト　 bt² + 　ナニ　 b²t – 　ヌ　 b³ )
が得られる。
　したがって、 S = T となるのは t = 　ネ　　ノ　 b のときである。

解答

サシス

　　g ( x ) – h ( x )
　　= x² – 3bx + 2b² = 0
を解いて、
　　x = b , 2b
よって、
　　α = b , β = 2b
である。

セソタ

それぞれの範囲で y = g ( x ) と y = h ( x ) のどちらが大きいか、位置関係に気をつける。

　いま、b ≦ x ≦ 2b の範囲において、 g ( x ) – h ( x ) ≦ 0 すなわち h ( x ) ≧ g ( x ) であるから、求める面積 S は、

$S = \int_{\alpha}^{\beta} \{ h ( x) - g(x) \} dx$

である。よって選択肢は②。　

　β = 2b ≦ x の範囲では、 g ( x ) ≧ h ( x ) であるから、求める面積 T は、

$T = \int_{\beta}^{t} \{ g ( x) - h(x) \} dx$

である。よって選択肢は①。

　最後に、

$\begin{align*} &S - T \\ &= \int_{\alpha}^{\beta} \{ h(x)-g(x) \} dx - \int_{\beta}^t \{ g(x) - h(x) \} dx \\ &=\left\{ \int_{\alpha}^{t} \{ h(x)-g(x) \} dx - \int_{\beta}^{t} \{ h(x)-g(x) \} dx \right\} + \int_{\beta}^t \{ h(x) - g(x) \} dx \\ &=\int_{\alpha}^{t} \{ h(x)-g(x) \} dx \end{align*}$

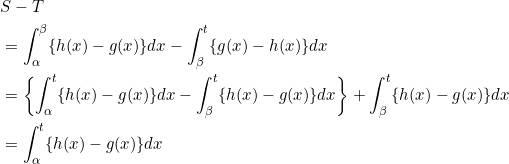
より、選択肢は②。

チツテトナニヌ

　あとは計算するだけです。 h ( x ) – g ( x ) は冒頭計算した g ( x ) – h ( x ) の符号を入れ替えるだけです。また、α = b に注意して、

$\begin{align*} &S - T \\ &=\int_{\alpha}^{t} \{ h(x)-g(x) \} dx \\ &=\int_b^t ( -x^2 +3bx -2b^2)dx \\ &=\left[ -\frac{1}{3}x^3 + \frac{3}{2}bx^2 - 2b^2x \right]_b^t \\ &=\bm{\frac{-1}{6}} (2t^3 -\bm{9}bt^2 +\bm{12}b^2t -\bm{5}b^3 ) \end{align*}$

となる。

ネノ

　S – T の計算結果のカッコ内がゼロ、すなわち
　　2t³ – 9bt² + 12b²t – 5b³ = 0
であればよい。
　カッコ内を因数分解できればよい。組み立て除法などを利用して、 x = 52b が求める答え。