2021年共通テスト(1/31)数学IIB 第2問[1]

2021年共通テスト(1/31) 数学IIB　>>数学IA
講評　第1問[1]　第1問[2]　第2問[1]

a を実数とし、 f ( x ) = ( x – a ) ( x – 2 ) とおく。また、 $\displaystyle F(x) = \int_0^x f(t) dt$ とする。

(1)　a = 1 のとき、 F ( x ) は x = 　ア　で極小になる。

(2)　a = 　イ　のとき、 F ( x ) はつねに増加する。また、 F ( 0 ) = 　ウ　であるから、 a = 　イ　のとき、 F ( 2 ) の値は　エ　である。

　エ　の解答群

⓪　0　　①　正　　②　負

(3)　a > 　イ　とする。 b を実数とし、 $\displaystyle G(x) = \int_b^x f(t)dt$ とおく。

　関数 y = G ( x ) のグラフは、 y = F ( x ) のグラフを　オ　方向に　カ　だけ平行移動したものと一致する。また、 G ( x ) は x = 　キ　で極大になり、 x = 　ク　で極小になる。
　G ( b ) = 　ケ　であるから、 b = 　キ　のとき、曲線 y = G ( x ) と x 軸との共有点の個数は　コ　個である。

　オ　の解答群

⓪　x軸　　①　y軸

　カ　の解答群

⓪　b　　①　-b　　②　F ( b )
③　- F ( b )　　④　F ( – b )　　⑤　- F ( – b )

解答

ア

　いま、　y = ( x – 1 ) ( x – 2 ) である。
　y ≧ 0 すなわち、 x ≦ 1 , 2 ≦ x の範囲では F ( x ) は増加し、 1 ≦ x ≦ 2 では F ( x ) は減少する。すなわち、 y = F ( x ) のグラフは以下のようになる。よって極小となるのは、 x = 2 のときである。

イ

　逆に、F ( x ) が常に増加するということはすべての x において y ≧ 0 であるということである。
　　y = ( x – a ) ( x – 2 ) ≧ 0
が常に成り立つということは、 y = ( x – a ) ( x – 2 ) のグラフと x 軸が接する、または交点が存在しないということである。
　それは a = 2 のときである。

　上記条件は、2自方程式 ( x – a ) ( x – 2 ) = 0 の解の個数が1個以下、ということだから、判別式を利用して、
　　( x – a ) ( x – 2 ) = x² – ( 2 + a ) x + 2a = 0 の判別式 D ≦ 0
としてもよい。
　　D = ( a + 2 )² – 4・2a
　　　= a² – 4a + 4
　　　= ( a – 2 )² ≦ 0
を解いて、 a = 2 としてもよい。ですが、図から明らかなことなので、上記解答が理解できるようになりましょう。

ウ

　積分範囲が 0 から 0 となるので、 $\displaystyle F(0) = \int_0^0 f(t) dt = \bm{0}$ である。

エ

　a = 2 のとき F ( x ) は常に増加であり、 f ( 0 ) = 0 から始まって常に増加ということから、 F ( 2 ) の値は①　正である。

オカ

　F ( x ) , G ( x ) の定義の式から、

$\begin{align*} F(x) &= \int_0^b f(t)dt + \int_b^x f(t)dt \\ &= F(b) + G(x) \end{align*}$

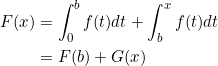
すなわち、
　　G ( x ) = F ( x ) – F ( b )
となる。よって、 y = G ( x ) のグラフは y = F ( x ) のグラフを ①　y 軸方向に ③　- F ( b ) だけ平行移動したものであるといえる。

キク

　y = G ( x ) のグラフは y = F ( x ) のグラフを y 軸方向に平行移動しただけであるから、極大極小を与える x の値は、 y = F ( x ) と変わらない。
　いま、 a > 2 であるから、y = F ( x ) のグラフは、（先程までと違い、） x = 2 のとき極大、 x = a のときが極小となる。

ケ

　積分範囲を考えて、 $\displaystyle G ( b) = \int_b^b f(t) dt = \bm{0}$ である。

コ

　いま、 b = 2 だとすれば、 G ( 2 ) = 0 が極大値ということだから、 y = G ( x ) のグラフは次のようになり、 x 軸との共有点の個数は 2 個となる。