解答
アイ
△A1C1B1 は ∠B1A1C1 = ∠B1C1A1 の二等辺三角形であり、
∠A1B1C1 = 108°
であるから、
∠A1C1B1 = ( 180° – 108° ) ÷ 2 = 36°
である。
ウ
A1A2 = a , B1C1 = 1 であり、A1A2 // B1C1 であるから、
![]()
である。
エオ
ウ = a なので、問題文の式より、
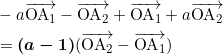
となる。
カキク
これも問題文の誘導より、求める値は、
A1A22 = a2 = 6 + 2√54 = 3 + √52……(a)
ケコサ
いま、
![]()
であり、いま、![]() であるから、
であるから、
![]()
より、
![]()
である。
シ
まず、問題文にある
![]()
を見るに、正五角形のある1つの頂点からそれぞれの辺に沿ったベクトルの内積は、この値になることが分かる。この値を b としておく。
問題文にある
![]()
であることを用いると、
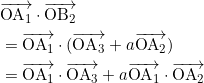
ここで、 ![]() と
と![]() はいずれも正五角形の隣り合う辺の内積であるから、その値は b となる。よって、求める値は
はいずれも正五角形の隣り合う辺の内積であるから、その値は b となる。よって、求める値は
b + ab = b ( 1 + a )
= 1 – √54 ✕ 3 + √52 = – 2 – 2√58 = – 1 – √54
である。よって解答は ⑨ である。
ス
前のページの問題文にある
![]()
であることを用いると、
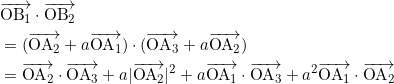
であり、先程と同様に、ここに出てくる内積はすべて b となるので、
b + a・1 + ab + a2b
= a + ( 1 + a + a2 ) b
となるので、(a)などの
= 1 + √52 + ( 1 + 1 + √52 + 3 + √52 ) ✕ 1 – √54
= 1 + √52 + ( 3 + √5 ) ✕ 1 – √54
= 1 + √52 + – 1 – √52
= 0
となるので、答えは ⓪ 0 である。
セ
四角形OB1DB2の4つの辺は、いずれも合同な正五角形の対角線であるから、すべて同じ長さである。ひし形または正方形である。
つぎに、先程の結果より、 ![]() より、
より、
∠B1OB2 = 90°
であるから、この四角形は ⓪ 正方形 である。

コメント