2018年センター数学IIB 第1問[2]

2018年センター数学IIB
　第1問[1]　第1問[2]　第2問[1][2]　第3問　第4問
　数学IIB講評　PDF　>>数学IA

　c を正の定数として、不等式

② $x^{\log_3 x} \geqq \left( \frac{x}{c} \right)^3$

を考える。

　3を底とする②の両辺の対数をとり、 t = log₃ x とおくと
　　t^ソ – 　タ　 t + 　タ　 log₃ c ≧ 0 ③
となる。ただし、対数 log_a b に対し、 a を底といい、 b を真数という。

　 $c = \sqrt[3]{9}$ のとき、②を満たす x の値の範囲を求めよう。③により
　　t ≦ 　チ　 , t ≧ 　ツ　
である。さらに、真数の条件を考えて
　　　テ　 < x ≦ 　ト　 , x ≧ 　ナ　
となる。

　次に、②が x > 　テ　の範囲でつねに成り立つような c の値の範囲を求めよう。
　 x が x > 　テ　の範囲を動くとき、 t のとり得る値の範囲は　ニ　である。　ニ　に当てはまるものを、次の⓪～③のうちから一つ選べ。

　⓪　正の実数全体　　①　負の実数全体
　②　実数全体　　　　③　1以外の実数全体

　この範囲の t に対して、③がつねに成り立つための必要十分条件は log₃ c ≧ 　ヌ　　ネ　である。すなわち、 c ≧ ^ノ√　ハヒ　である。

解答

ソタ

　問題文の指示の通り計算すると、

$\begin{align*} &\log_3 x^{\log_3 x} \geqq \log_3 \left( \frac{x}{c} \right)^3 \\ &(\log_3 x)\cdot(\log_3 x) \geqq 3 ( \log_3 x - \log_3 - c ) \\ &t^{\bm{2}} - \bm{3}t + 3\log_3 c \geqq 0 \end{align*}$

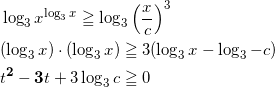
となる。

チツテトナ

　 $c = \sqrt[3]{9} = 3^{2/3}$ を代入して、

$\begin{align*} t^2 -3t + 3 \log_3 3^{2/3} \geqq 0 \\ t^2 - 3t + 2 \geqq 0 \\ (t-1)(t-2) \geqq 0 \end{align*}$

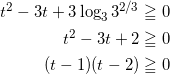
より、 t ≦ 1 , t ≧ 2 となる。

　さらに、 x = 3^t であるから、真数条件を含めて考えると、
　　0 < x ≦ 3 , 9 ≦ x
となる。

ニ

　t = log₃ x が x > 0 で取りうる値は ② 実数全体 である。

ヌネノハヒ

　③が常に成り立つということは、2次方程式 $t^2 -3t + 3\log_3 c = 0$ の判別式 D ≦ 0 であるということなので、

$9 - 4\cdot 3 \log_3 c \leqq 0$

を解いて、

$\log_3 c \geqq \bm{\frac{3}{4}}$

すなわち、

$c \geqq 3^{3/4} = \bm{ \sqrt[4]{27} }$

となる。