2018年センター数学IIB 第4問

2018年センター数学IIB
　第1問[1]　第1問[2]　第2問　第3問　第4問
　数学IIB講評　PDF　>>数学IA

解答

ア

$\overrightarrow{\text{AB}} = \overrightarrow{\text{FB}} - \overrightarrow{\text{FA}} = \overrightarrow{q} - \overrightarrow{p}$

であるから、解答は ② である。

イ

$\overrightarrow{\text{AB}} = \overrightarrow{q} - \overrightarrow{p}$

より、

$| \overrightarrow{\text{AB}} |^2 = |\overrightarrow{p}|^2 - \bm{2} \overrightarrow{p} \cdot \overrightarrow{q} + | \overrightarrow{q}|^2$

となる。

ウエオカ

(※) $\begin{align*} \overrightarrow{\text{FD}} &= \overrightarrow{\text{FA}} + \overrightarrow{\text{AD}} \\ &= \overrightarrow{\text{FA}} + \frac{1}{4}\overrightarrow{\text{AB}} \\ &= \overrightarrow{p} + \frac{1}{4} ( \overrightarrow{q} -\overrightarrow{p} ) \\ &= \bm{\frac{3}{4}} \overrightarrow{p} + \bm{\frac{1}{4}} \overrightarrow{q} \end{align*}$

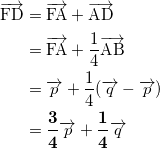
点Dは線分ABを1:3に内分する点なので、任意の点Xからの2つのベクトルを用いて、

$\overrightarrow{\text{FD}} = \frac{3\overrightarrow{\text{XA}} + \overrightarrow{\text{XN}}}{4}$

が成り立ちます。ここで X = F としたものがこの答えです。

キクケ

　 $\overrightarrow{\text{FD}}$ について(※)式から、

$\frac{3}{4} \overrightarrow{p} + \frac{1}{4} \overrightarrow{q} = s \overrightarrow{r}$

が成り立つので、これをを変形して、

③ $\overrightarrow{q} = \bm{-3} \overrightarrow{p} + \bm{4} s\overrightarrow{r}$

となる。

コサシ

　次に $\overrightarrow{\text{FE}}$ について着目すると、点 E は線分BCを a : ( 1 – a ) に内分する点なので、

$\overrightarrow{\text{FE}} = a \overrightarrow{\text{FC}} + ( 1-a )\overrightarrow{\text{FB}}$

となり、これより、

$\overrightarrow{\text{FE}} = a \overrightarrow{r} + ( 1 - a ) \overrightarrow{q} = t\overrightarrow{p}$

となり、これを $\overrightarrow{q}$ について解いて、

④ $\overrightarrow{q} = \frac{t}{\bm{1-a}} \overrightarrow{p} - \frac{\bm{a}}{1-a} \overrightarrow{r}$

となる。

スセソタチ

　③と④より、

$\frac{t}{1-a} = -3 , \frac{a}{1-a} = -4s$

より、

(※※) $s = \bm{\frac{-a}{4(1-a)}} , t =\bm{ -3(1-a)}$

となる。

ツテ

$\begin{align*} |\overrightarrow{\text{BE}}|^2 &= | \overrightarrow{\text{FE}} - \overrightarrow{\text{FB}} |^2 \\ &=|t\overrightarrow{p} - \overrightarrow{q} |^2 \\ &= t^2 |\overrightarrow{p}|^2 - 2t \overrightarrow{p} \cdot \overrightarrow{q} + | \overrightarrow{q}|^2 \end{align*}$

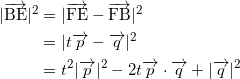
となり、ここに、(※※)を代入して

$|\overrightarrow{\text{BE}}|^2 = \bm{9}( 1-a)^2 + \bm{6}(1-a) \overrightarrow{p} \cdot \overrightarrow{q} + |\overrightarrow{q}|^2$

となる。

トナニヌ

$|\overrightarrow{\text{AB}}|^2 = 1 - 2 \overrightarrow{p} \cdot \overrightarrow{q} + |\overrightarrow{q}|^2$

と

$|\overrightarrow{\text{BE}}|^2 = \bm{9}( 1-a)^2 + \bm{6}(1-a) \overrightarrow{p} \cdot \overrightarrow{q} + |\overrightarrow{q}|^2$

より、

$\begin{align*} & 1 - 2\overrightarrow{p} \cdot \overrightarrow{q} + |\overrightarrow{q}|^2 = 9 ( 1-a)^2 + 6(1-a)\overrightarrow{p} \cdot \overrightarrow{q} + |\overrightarrow{q}|^2 \\ &(6-6a+2) \overrightarrow{p} \cdot \overrightarrow{q} = 1 - 9 ( 1-a)^2 \\ &(8-6a) \overrightarrow{p} \cdot \overrightarrow{q} = 9a^2 -18a + 8 \\ &\overrightarrow{p} \cdot \overrightarrow{q} = \frac{3}{2}a - 1 = \bm{\frac{3a-2}{2}} \end{align*}$

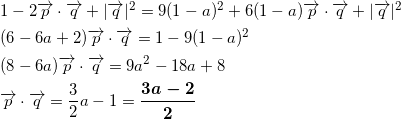
となる。（最後は分母を分子で割り算をします。整式の割り算。）