2021年共通テスト数学IIB 第1問[2]

2021年共通テスト数学IIB　>>数学IA
講評　第1問[1]　第1問[2]　第2問　第4問　第5問

解答

セソ

　x = 0 を代入して、

$\begin{align*} f(0) &= \frac{2^0 + 2^{-0}}{2} = \frac{1+1}{2} =\bm{1} \\ g(0) &= \frac{2^0 - 2^{-0}}{2} = \frac{1-1}{2} = \bm{0} \end{align*}$

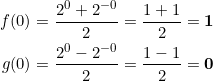
となる。

タチ

　相加相乗の不等式より、

$\frac{2^x+2^{-x}}{2} \geqq \sqrt{2^x \cdot 2^{-x}} = 1$

が成り立つ。等号成立は 2^x = 2^-x より x = 0 のときで、このとき最小値 1 を取ることが言える。

ツテ

　　g ( x ) = 2^x + 2^-x2 = -2
より、
　　2^x + 2^-x = -4
である。 2^x = t ( > 0 ) とおいて整理すると、
　　t² + 4t – 1 = 0
を解いて、 t = -2 + √5 となる。よって、
　　x = log₂( √5 – 2 )
である。

トナニヌ

　一つずつ実際に計算してみる。
　　f ( -x ) = 2^-x + 2^x2 = f(x)
　　g ( -x ) = 2^-x – 2^x2 = – 2^x – 2^-x2 = – g ( x )
　　{ f ( x ) }² – { g ( x ) }² = 2^2x + 2 + 2^-2x4 – 2^2x – 2 + 2^-2x4 = 1
となる。最後は、
　　g ( 2x ) = 2^2x – 2^-2x2
　　f ( x ) g ( x ) = 2^2x – 2^-2x4
であるから、
　　g ( 2x ) = 2 f ( x ) g ( x )
である。

2021年共通テスト数学IIB 第1問[2]

解答

セソ

タチ

ツテ

トナニヌ

ネ

コメント