(1) 直線 l : y = ( a2 – 2a – 8 ) x + a の傾きが負となるのは、 a の値の範囲が
アイ < a < イ
のときである。
(2) a2 – 2a – 8 ≠ 0 とし、(1)の直線 l と x 軸の交点の x 座標を b とする。
a > 0 の場合、 b > 0 となるのは エ < a < オ のときである。
a ≦ 0 の場合、 b > 0 となるのは a < カキ のときである。
また、 a = √3 のとき
b = ク √ ケ – コ サシ
である。
解答
アイウ
傾きが負なので、
a2 – 2a – 8 < 0
( a – 4 ) ( a + 2 ) < 0
より、 -2 < a < 4 である。
エオカキ
a > 0 ということはy切片が正ということ。x軸との交点がプラスになるためには、傾きが負であればよい。
よって、(1)とあわせて、
0 < a < 4
である。
同様に、 a ≦ 0 のときはy切片が負(もしくは0)ということ、x軸との交点がプラスになるためには、傾きが正であればよいので、 a < -2 または 4 < a ということで、条件である a ≦ 0 と合わせて、
a < -2
であればよい。
クケコサシ
求めるのは x軸との交点 b であるから、(1)の直線の式において、 y = 0 , x = b として方程式を解く。
a = √3 を素直に代入して、
![]()
より、
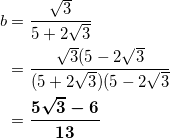
である。

コメント