真分数を分母の小さい順に、分母が同じ場合には分子の小さい順に並べてできる数列
![]()
を { an } とする。真分数とは、分子と分母がともに自然数で、分子が分母より小さい分数のことであり、上の数列では、約分できる形の分数も含めて並べている。以下の問題に分数形で解答する場合は、回答上の注意にもあるように、それ以上約分できない形で答えよ。
(1) a15 = ア イ である。また、分母に初めて 8 が現れる項は、 aウエ である。
(2) k を 2 以上の自然数とする。数列 { an } において、 ![]() が初めて現れる項を第 Mk 項とし、
が初めて現れる項を第 Mk 項とし、 ![]() が初めて現れる項を第 Nk 項とすると
が初めて現れる項を第 Nk 項とすると
Mk = オ カ k2 – キ ク k + ケ
Nk = コ サ k2 – シ ス k
である。よって、 a104 = セソ タチ である。
(3) k を 2 以上の自然数とする。数列 { an } の第 Mk 項から第 Nk 項までの和は、 ツ テ k – ト ナ である。したがって、数列 { an } の初項から第 Nk 項までの和は
ニ ヌ k2 – ネ ノ k
である。よって
![]() = ハヒフ ヘホ
= ハヒフ ヘホ
である。
解答
アイウエ
まずはじめは、様子を見るためにも書き出します。あとで便利なように、“群”に分けます。
![Rendered by QuickLaTeX.com \[ \frac{1}{2} \left| \frac{1}{3} , \frac{2}{3} \right| \frac{1}{4} , \frac{2}{4} ,\frac{3}{4} \left| \frac{1}{5} , \frac{2}{5} , \frac{3}{5} , \frac{4}{5} \right| \frac{1}{6} , \frac{2}{6} ,\frac{3}{6} , \frac{4}{6} , \underbrace{\frac{5}{6}}_{a_{15}} \left| \frac{1}{7} , \frac{2}{7} ,\frac{3}{7} , \frac{4}{7} , \frac{5}{7} , \frac{6}{7} \right| \underbrace{\frac{1}{8}}_{a_{22}} \cdots \]](http://izu-mix.com/math/wp-content/ql-cache/quicklatex.com-e985da808cf4beb57210f6d44e2d1b38_l3.png)
となることより、![]() であり、はじめて分母に8が現れる項は a22である。
であり、はじめて分母に8が現れる項は a22である。
オカキクケコサシス
を確認してから解くのがコツ!
■第 m 郡の性質
第 m 群の性質は、「分母が m + 1 となる分数が、![]() まで集まったもの」といえる。逆に、分母が k のものは、第 k – 1 群ともいえる。
まで集まったもの」といえる。逆に、分母が k のものは、第 k – 1 群ともいえる。
■第 m 郡の項の数
第 m 群の項数は、具体例を見てもわかるが、m 個である。
■第 m 群の初項/末項は初めから数えて何項目か
さきに第 m 項の末項は初めから数えて何項目かを考える。これは、第 1 群から第 m 群までの群の項数を足し合わせたものである。群の項数はうえで求めたとおりで、
![]() ……①
……①
となる。
最後に、第 m 群の初項は、第 m – 1 群の末項の次の番目になる。第 m – 1 群の末項は、①の m を m – 1 に置き換えたものだから、
![]() ……②
……②
となる。
さて、問題文にある Mk とは、第 k – 1 群の初項のことである。それは②の m を k – 1 に置き換えれば良いので、
![]()
となる。
つぎに、問題文にある Nk とは、第 k – 1 群の末項のことであり、それは①の m を k – 1 に置き換えれば良いので、
![]()
となる。
セソタチ
第104項に近いあたりで、ちょうどある群の末項になるものを探す。(初項になるものを探しても良い。)
①式に m = 14 を代入すると、 ![]() となるので、第 14 群の末項は初めから数えて 105 項目であることが分かる。第 m 項の最後の項は、
となるので、第 14 群の末項は初めから数えて 105 項目であることが分かる。第 m 項の最後の項は、![]() であるから、
であるから、
![]()
である。よって、![]() である。
である。
ツテトナ
第 Mk 項から第 Nk 項の和は、
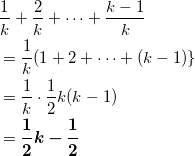
となる。
これは、分母が k である群(第 k – 1 群)のすべての分数の和ということである。
ニヌネノ
今求めたものを、 k を 1 から k まで足し合わせればよい。式で表すと、
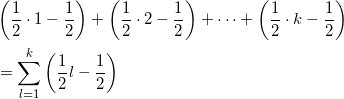
となるのでこれを計算して、
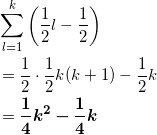
となる。
ハヒフヘホ
先ほど見たように、![]() は、
は、 ![]() である。すなわち、
である。すなわち、
![Rendered by QuickLaTeX.com \[ \sum_{n=1}^{105} a_n = \frac{1}{4} \cdot 15^2 - \frac{1}{4} \cdot 15 = \frac{105}{2} \]](http://izu-mix.com/math/wp-content/ql-cache/quicklatex.com-d8368a7f87c0cdb85dec41c59e180595_l3.png)
となる。求める値は、![]() から a104 と a105 を引いた値なので、
から a104 と a105 を引いた値なので、
![Rendered by QuickLaTeX.com \[ \sum_{n=1}^{103} a_n = \frac{105}{2} - (a_{104} + a_{105}) = \frac{105}{2} - \frac{13+14}{15} = \bm{\frac{507}{10}} \]](http://izu-mix.com/math/wp-content/ql-cache/quicklatex.com-e13b546300cd07613ed42da4a7eb8878_l3.png)
となる。

コメント